练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知Rt△ABC中，∠C=90°，∠A=50°，AB=2，则AC=（　　）
    A．2sin50°B．2sin40°C．2tan50°D．2tan40°

    分析 根据在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，可得答案．

    解答 解：由Rt△ABC中，∠C=90°，∠A=50°，得
    ∠B=40°，
    由sin∠B=$\frac{AC}{AB}$，得
    AC=ABsin∠B=2sin40°，
    故选：B．

    点评 本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．有48张扑克牌，牌面朝下，随机抽出一张记下花色后放回；洗牌后再这样抽，经历多次试验得到随机抽出一张牌是红桃的概率为$\frac{1}{4}$，则红桃牌大约有12张．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：（x-2y）2+（2x3-14x2y+8xy2）÷（-2x），其中x=-$\frac{2}{3}$，y=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，四边形ABCO是平行四边形，AB=4，OB=2，抛物线过A、B、C三点，与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动，运动到点A停止，同时一动点Q从点D出发，以每秒3个单位长度的速度沿DC向点C运动，与点P同时停止，设点P运动的时间为t秒．
    （1）求抛物线的解析式；
    （2）在抛物线对称轴上找一点M，使点M到B，C两点的距离之和最小，求出点M的坐标；
    （3）若抛物线的对称轴与AB交于点E，与x轴交于点F，求当t为何值时，四边形POQE是等腰梯形？
    （4）求当t为何值时，以P、B、O为顶点的三角形与以点Q、B、O为顶点的三角形相似？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

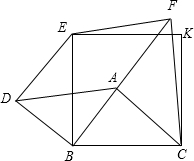    18．已知，A是正方形EKCB内的任意点，分别以AB、AC为直角边，按如图方式作等腰直角三角形，即Rt△ABD、Rt△FAC，又∠ABD=∠FAC=90°，连接DE、EF．
    （1）求证：四边形ADEF是平行四边形；
    （2）当△ABC满足什么条件时，四边形ADEF是菱形？请说明理由．
    （3）进一步探究：四边形ADEF与四边形EKCB相似的可能性，并求其相似比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知抛物线的顶点坐标为（1，-2），且抛物线经过点（2，3），求抛物线的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．把下列各数填入相应的集合内：
    -7，0.32，$\frac{1}{3}$，46，0，$\sqrt{8}$，$\sqrt{\frac{1}{2}}$，$\root{3}{216}$，-$\frac{\sqrt{2}}{2}$
    （1）有理数集合：{$\sqrt{8}$，$\sqrt{\frac{1}{2}}$，-$\frac{\sqrt{2}}{2}$…}
    （2）无理数集合：{-7，0.32，$\frac{1}{3}$，46，0，$\root{3}{216}$…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

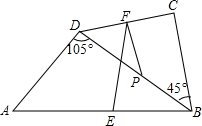    12．如图，点P是四边形ABCD的对角线BD的中点，E，F分别是AB，CD的中点，AD=BC，∠CBD=45°．∠ADB=105°，试探究EF与PF之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如下表，方程1、方程2、方程3…是按照一定的规律排列的一列方程，解方程3，并将它的解填在表中的空白处．
    序号　方程　方程的解　
    　1x2+2x-3=0　x1=1　x2=-3　
    2　x2+4x-12=0　x1=2　x2=-6　
    3　x2+6x-27=0　x1=3x2=-9
    …………
    （1）请写出这列方程中第m个方程，并写出它的解．
    （2）用你探究的规律解方程x2-8x-20=0．

    查看答案和解析>>

    同步练习册答案