
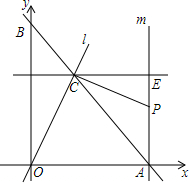
 如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.
如图,直线y=-x+$\sqrt{2}$分别交x轴、y轴于A、B两点,经过点A的直线m⊥x轴,直线l经过原点O交线段AB于点C,过点C作OC的垂线,与直线m相交于点P,现将直线l绕O点旋转,使交点C在线段AB上由点B向点A方向运动.分析 (1)把x=0,y=0代入y=-x+$\sqrt{2}$解答即可;
(2)DE∥x轴,m⊥x轴,根据ASA证△ODC≌△CEP即可;
(3)①根据Rt△BDC中的勾股定理进行解答即可;
②根据等腰三角形和等腰直角三角形的性质进行解答.
解答 解:(1)把x=0,y=0代入y=-x+$\sqrt{2}$,可得:点A($\sqrt{2}$,0),B(0,$\sqrt{2}$);
故答案为:A($\sqrt{2}$,0),B(0,$\sqrt{2}$);
(2)∵DE∥x轴,m⊥x轴,
∴m⊥DE,DE⊥y轴,
∴∠ODE=∠CEP=90°,
∵OC⊥CP,
∴∠OCP=90°,
∴∠DCO+∠ECP=180°-∠OCP=90°,
∴∠DCO+∠DOC=90°,
∴∠ECP=∠DOC,
∵$OA=OB=\sqrt{2}$,
∴∠ABO=∠BAO,
∵DE∥x轴,
∴∠BCD=∠BAO,
∴∠ABO=∠BCD,
∴BD=CD,AE∥y轴,由平移性质得:OA=DE,
∴OB=DE,OB-BD=DE-CD,
∴OD=CE,
在△ODC与△CEP中,
$\left\{\begin{array}{l}{∠CDO=∠CEP}\\{OD=CE}\\{∠DOC=∠ECP}\end{array}\right.$,
∴△ODC≌△CEP(ASA);
(3)①∵$BC=\sqrt{2}$t,BD=CD,
在Rt△BDC中,BD2+CD2=BC2
∴BD=CD=t,OA=OB=$\sqrt{2}$,DO=BO-BD=$\sqrt{2}$-t,EA=DO=$\sqrt{2}$-t,$OA=OB=\sqrt{2}$-t,EP=CD=t,AP=EA-EP=$\sqrt{2}$-2t,
在Rt△AOB中,AO2+BO2=AB2
∴OA=2$a=\sqrt{2}-2t$(0≤t≤2),
②当t=0时,△PAC是等腰直角三角形$PB=PA=\sqrt{2}$
∴即点坐标是:P($\sqrt{2}$,$\sqrt{2}$),PA=AC,则$|{\sqrt{2}-2t}|=2-\sqrt{2}$t
解得t=1或t=-1(舍去)
∴当t=1时,△PAC是等腰三角形
即点坐标是:P($\sqrt{2}$,$\sqrt{2}$-2),
∴当t=0或1时,△PAC为等腰三角形,
点P的坐标为:P($\sqrt{2}$,$\sqrt{2}$)或P($\sqrt{2}$,$\sqrt{2}$-2).
点评 主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数的性质和点的意义表示出相应的线段的长度,再结合三角形全等和等腰三角形的性质求解.试题中贯穿了方程思想和数形结合的思想,请注意体会.


科目:初中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知一个角是它的余角的一半,求这个角的度数;
(1)已知一个角是它的余角的一半,求这个角的度数;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
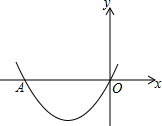 如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.
如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
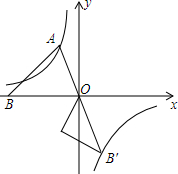 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.那么需要多少张餐桌拼在一起可坐90人用餐?若设需要这样的餐桌x张,可列方程为4x+2=90.
一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.那么需要多少张餐桌拼在一起可坐90人用餐?若设需要这样的餐桌x张,可列方程为4x+2=90.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com