



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=
如图,在△ABC中,以AC为直径的⊙O交BC于D,过C作⊙O的切线,交AB的延长线于P,∠PCB=| 1 |
| 2 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某工厂拟建一座平面图形为矩形且占地面积为200平方米的三级污水处理池,如图所示.由于地形限制,三级污水处理池的长、宽都不能超过16米,高h为2m.如果池的外围墙建造单价为每平方米400元,中间两条隔墙建造单价为每平方米300元(隔墙厚度不计),池底建造单价为每平方米80元(池墙的厚度忽略不计).求:当三级污水处理池的总造价为80000元时,池长x为多少?
某工厂拟建一座平面图形为矩形且占地面积为200平方米的三级污水处理池,如图所示.由于地形限制,三级污水处理池的长、宽都不能超过16米,高h为2m.如果池的外围墙建造单价为每平方米400元,中间两条隔墙建造单价为每平方米300元(隔墙厚度不计),池底建造单价为每平方米80元(池墙的厚度忽略不计).求:当三级污水处理池的总造价为80000元时,池长x为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| |||||||||||||
B、
| |||||||||||||
C、
| |||||||||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
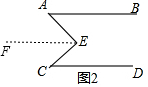
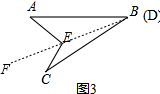
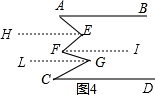
 如图,下列推论及所注理由正确的是( )
如图,下列推论及所注理由正确的是( )| A、∵∠1=∠B,∴DE∥BC(两直线平行,同位角相等) |
| B、∵∠2=∠C,∴DE∥BC(两直线平行,同位角相等) |
| C、∵∠2+∠3+∠B=180°,∴DE∥BC(同旁内角互补,两直线平行) |
| D、∵∠4=∠1,∴DE∥BC(对顶角相等) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com