
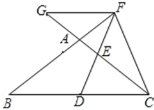
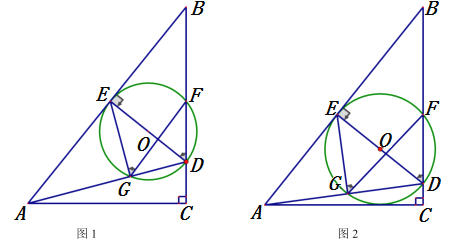
【题目】如图,在△ABC 中,AB =AC,点D在BC上,点F在BA的延长线上,FD =FC,点E是AC与DF的交点,且ED =EF,FG∥BC交CA的延长线于点G.
(1)∠BFD =∠GCF 吗?说明理由;
(2)求证:△GEF ≌△CED;
(3)求证:BD =DC.
【答案】(1)∠BFD=∠GCF,理由见解析;(2)证明见解析;(3)证明见解析
【解析】
(1)根据AB=AC得出∠B=∠BCA,再利用FD=FC得出∠FDC=∠DCF,最后结合三角形外角性质进一步证明即可;
(2)利用平行线性质得出∠GFE=∠CDE,然后结合题意根据“ASA”进一步证明结论即可;
(3)首先根据题意得出∠B=∠G,然后进一步证明△GFC△BDF,由此得出GF=BD,再根据△GEF△CED得出GF=CD,据此进一步证明结论即可.
(1)∠BFD=∠GCF,理由如下:
∵AB=AC,
∴∠B=∠BCA,
∵FD=FC,
∴∠FDC=∠DCF,
∵∠BFD=∠FDC∠B,∠GCF=∠DCF∠BCA,
∴∠BFD=∠GCF;
(2)∵FG∥BC,
∴∠GFE=∠CDE,
在△GEF和△CED中,
∵∠GFE=∠CDE,ED=EF,∠FEG=∠DEC,
∴△GEF△CED(ASA);
(3)∵FG∥BC,
∴∠G=∠BCA,
∵∠B=BCA,
∴∠B=∠G,
在△GFC和△BDF中,
∵∠B=∠G,∠BFD=∠GCF,FD=FC,
∴△GFC△BDF(AAS),
∴GF=BD,
∵△GEF△CED,
∴GF=CD,
∴BD=DC.


科目:初中数学 来源: 题型:
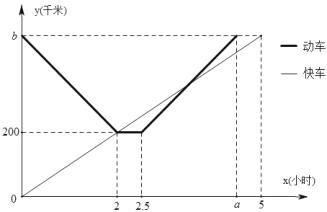
【题目】某地区在同一直线上依次有甲、乙、丙三座城市一列快车从甲市出发匀速行驶开往丙市,一列动车从丙市出发匀速行驶往返于乙、丙两座城市,两列火车同时出发.如图是两列火车距甲市的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象,请你结合图像信息解决下列问题:
(小时)之间的函数图象,请你结合图像信息解决下列问题:
(1)直接写出:甲、乙两市相距 千米,图像中![]() 的值为 ,
的值为 ,![]() 的值 ;
的值 ;
(2)求动车从乙地返回多长时间时与快车相遇?
(3)请直接写出快车出发多长时间两列火车(都在行驶时)相距30千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
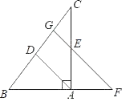
【题目】如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过AC的中点E作FG∥AD,交BA的延长线于点F,交BC于点G,
(1)求证:AE=AF;
(2)若BC=![]() AB,AF=3,求BC的长.
AB,AF=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:
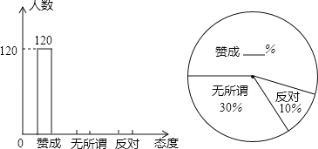
根据上述信息,解答下列问题:
(1)抽取的学生人数为 ;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一个动点,作
上一个动点,作![]() ,交直角边
,交直角边![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .连结
.连结![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)求证:![]() ;
;
(3)如图2,当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的直径;
的直径;
(4)若以![]() 为顶点的三角形是等腰三角形时,求所有满足条件的
为顶点的三角形是等腰三角形时,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:把函数![]() 的图像绕点
的图像绕点![]() 旋转180°,得到新函数
旋转180°,得到新函数![]() 的图像,我们称
的图像,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图像的对称轴为直线
的图像的对称轴为直线![]() .例如:当
.例如:当![]() 时,函数
时,函数![]() 关于点
关于点![]() 的相关函数为
的相关函数为![]() .
.
(1)填空:![]() 的值为________(用含
的值为________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,
时,![]() 的图像与
的图像与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 绕原点
绕原点![]() 顺时针旋转90°,得到它的对应线段
顺时针旋转90°,得到它的对应线段![]() .若线段
.若线段![]() 与
与![]() 的图像有公共点,结合函数图像,求
的图像有公共点,结合函数图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com