
【题目】某地区在同一直线上依次有甲、乙、丙三座城市一列快车从甲市出发匀速行驶开往丙市,一列动车从丙市出发匀速行驶往返于乙、丙两座城市,两列火车同时出发.如图是两列火车距甲市的路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象,请你结合图像信息解决下列问题:
(小时)之间的函数图象,请你结合图像信息解决下列问题:
(1)直接写出:甲、乙两市相距 千米,图像中![]() 的值为 ,
的值为 ,![]() 的值 ;
的值 ;
(2)求动车从乙地返回多长时间时与快车相遇?
(3)请直接写出快车出发多长时间两列火车(都在行驶时)相距30千米?
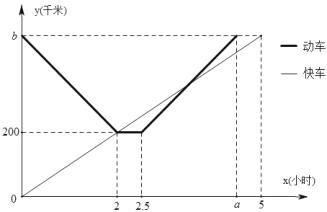
【答案】(1)200,4.5,500;(2)1小时;(3)快车出发1.88小时或2.9小时或4.1小时两列火车(都在行驶时)相距30千米
【解析】
(1)由图可知:当x=2时,y=200,此时动车停在乙市,所以甲、乙两市相距200千米,动车从丙市出发匀速行驶往返于乙、丙两座城市,动车从丙市出发匀速行驶到乙市所用的时间与动车从乙市出发匀速行驶到丙市所用的时间相同,都为2小时,可得a=2.5+2=4.5,快车2小时行驶了200千米,可求得快车速度,
b=100×5=500
(2)设快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=kx,
把点(2,200)的坐标代入到y=kx中,求得函数解析式y=100x.
设动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k1x+b1,把点(2.5,200)、(4.5,500)的坐标分别代入到y=k1x+b1中,求得函数解析式y=150x-175,求出方程组![]() 的解为
的解为![]() ,因为3.5-2.5=1(小时),可得动车从乙地返回1小时时与快车相遇.
,因为3.5-2.5=1(小时),可得动车从乙地返回1小时时与快车相遇.
(3)设动车丙市出发时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k2x+b2,把点(2,200)、(0,500)的坐标分别代入到y=k2x+b2中,解得y=-150x+500,由(2)可知:快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=100x(0≤x≤5),动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=150x-175(2.5≤x≤4.5),
当0≤x≤2时,-150x+500-100x=30,解得x=![]() =1.88;
=1.88;
当2.5≤x≤3.5时,100x-(150x-175)=30,解得x=![]() =2.9;
=2.9;
当3.5≤x≤4.5时,150x-175-100x=30,解得x=![]() =4.1
=4.1
综上所述,快车出发1.88小时或2.9小时或4.1小时两列火车(都在行驶时)相距30千米.
(1)由图可知:当x=2时,y=200,此时动车停在乙市
∴甲、乙两市相距200千米,
∵动车从丙市出发匀速行驶往返于乙、丙两座城市,
∴动车从丙市出发匀速行驶到乙市所用的时间与动车从乙市出发匀速行驶到丙市所用的时间相同,都为2小时,
∴a=2.5+2=4.5
由图可知:快车2小时行驶了200千米
∴快车的速度为:200÷2=100(千米/时)
∴100×5=500(千米)
∴b=500
故答案为:200,4.5,500
(2)设快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=kx,
把点(2,200)的坐标代入到y=kx中,
得:200=2k,
解得k=100,
∴快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=100x(0≤x≤5),
设动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k1x+b1,把点(2.5,200)、(4.5,500)的坐标分别代入到y=k1x+b1中,得: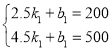 ,
,
解得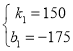 ,
,
∴动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=150x-175(2.5≤x≤4.5),
∵方程组![]() 的解为
的解为![]()
∴3.5-2.5=1(小时)
∴动车从乙地返回1小时时与快车相遇;
(3)设动车丙市出发时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=k2x+b2,把点(2,200)、(0,500)的坐标分别代入到y=k2x+b2中,得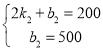 ,
,
解得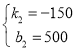 ,
,
∴动车丙市出发时,距甲市的路程(千米)与行驶时间(小时)之间的函数关系式为y=-150x+500,
由(2)可知:快车距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=100x(0≤x≤5)
动车从乙地返回时,距甲市的路程y(千米)与行驶时间x(小时)之间的函数关系式为y=150x-175(2.5≤x≤4.5),
当0≤x≤2时,-150x+500-100x=30,解得x=![]() =1.88;
=1.88;
当2.5≤x≤3.5时,100x-(150x-175)=30,解得x=![]() =2.9;
=2.9;
当3.5≤x≤4.5时,150x-175-100x=30,解得x=![]() =4.1
=4.1
综上所述,快车出发1.88小时或2.9小时或4.1小时两列火车(都在行驶时)相距30千米.


科目:初中数学 来源: 题型:
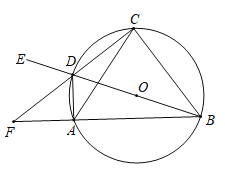
【题目】如图,⊙![]() 是四边形
是四边形![]() 的外接圆,
的外接圆,![]() 是四边形
是四边形![]() 的对角线, BD经过圆心O,点
的对角线, BD经过圆心O,点![]() 在BD的延长线上,BA与CD的延长线交于点F,DF平分
在BD的延长线上,BA与CD的延长线交于点F,DF平分![]()
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,⊙
,⊙![]() 半径为5,求
半径为5,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
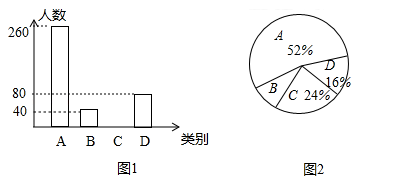
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了建设社会主义新农村,我市积极推进“行政村通畅工程”,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造.下面能反映该工程改造道路里程![]() (公里)与时间
(公里)与时间![]() (天)的函数关系大致的图像是( ).
(天)的函数关系大致的图像是( ).
A. B.
B.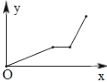 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如下尚不完整的统计图表:请根据以上信息解答下列问题:
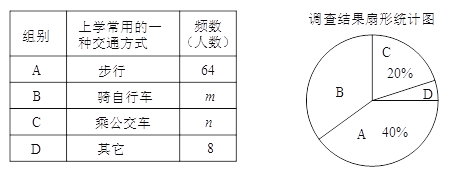
(1)参与本次调查的学生共有 人;
(2)统计表中,m= ,n= ;扇形统计图中,B组所对应的圆心角的度数为 ;
(3)若该校共有1500名学生,请估计全校骑自行车上学的学生人数;
(4)该小组据此次调查结果向学校建议扩建学生车棚,若平均每4平方米能停放5辆自行车,请估计在现有300平方米车棚的基础上,至少还需要扩建多少平方米才能满足学生停车需求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个不透明的布袋,甲袋中装有1个红球、3个黄球,乙袋中装有2个红球,1个绿球,小球除颜色外无其它区别;从甲袋中随机摸出一个小球,从乙袋中随机摸出一个小球,两球都为红球的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣2,5),与x轴相交于B(﹣1,0),C(3,0)两点.
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;

查看答案和解析>>
科目:初中数学 来源: 题型:
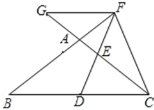
【题目】如图,在△ABC 中,AB =AC,点D在BC上,点F在BA的延长线上,FD =FC,点E是AC与DF的交点,且ED =EF,FG∥BC交CA的延长线于点G.
(1)∠BFD =∠GCF 吗?说明理由;
(2)求证:△GEF ≌△CED;
(3)求证:BD =DC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com