练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图：一块长10米，宽8米的地毯，为美观设计了两横、两纵的条纹，已知条纹的宽度相同，条纹外的部分占整个地毯面积的.

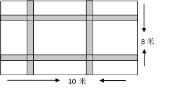
    （1）求条纹的宽度；

    （2）如果地毯配色条纹部分每平方米造价200元，其余部分每平方米造价100元，求地毯的总造价.

    【答案】（1）米；（2）9700元.

    【解析】

    （1）根据条纹外的部分占整个地毯面积的，设条纹宽度为x米，根据图形可列方程，解得再检验即可得出答案；

    （2）根据已知总面积，已知条纹外的部分占整个地毯面积的，可分别求出条纹所占面积以及其余所占面积，再分别乘以每平方米的造价最后相加即可得出总造价.

    解：（1）设条纹宽度为x米. 依题意可得：

    解得：，

    ∵

    ∴不符合题意舍去，

    ∴

    答：条纹的宽度为米.

    （2）依题意可得：（元）

    答：地毯的总造价为9700元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB＝10，AD＝4，点E从D向C以每秒1个单位的速度运动，以AE为一边在AE的左上方作正方形AEFG，同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动，当点F落在直线MN上，设运动的时间为t，则t的值为( )

    A.1B.C.4D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE，连接OC．

    （1）求证：DE是⊙O的切线；

    （2）若⊙O半径为4，∠D=30°，求图中阴影部分的面积（结果用含π和根号的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市茶叶专卖店销售某品牌茶叶，其进价为每千克 240 元，按每千克 400 元出售，平均每周可售出 200 千克，后来经过市场调查发现，单价每降低 10 元，则平均每周的销售量可增加 40 千克，若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元，请回答：

    （1）每千克茶叶应降价多少元？

    （2）在平均每周获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的 几折出售？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的方程有两个实数根、．

    （1）求实数k的取值范围；

    （2）若、满足，求实数的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知在△ABC中，∠B=90°，AB=6cm，BC=12cm，点Q从点A开始沿AB边向点B以1cm/s的速度移动，点P从点B开始沿BC边向点C以2cm/s的速度移动．

    （1）如果Q、P分别从A、B两点出发，那么几秒后，△PBQ的面积等于8cm2？

    （2）在（1）中，△PBQ的面积能否等于10cm2？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，直线y＝kx+b（k，b为常数）分别与x轴、y轴交于点A（﹣4，0），B（0，3），抛物线y＝﹣x2+4x+1与y轴交于点C，点E在抛物线y＝﹣x2+4x+1的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（　　）

    A.2B.4C.2.5D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着生活水平的提高,老年人的文化娱乐活动也越来越丰富,某街道在参加文体活动的560名老人中随机抽取了部分人调查他们平常每天参加文体活动的时间,并绘制了如图所示的扇形统计图和条形统计图,请根据图中信息,回答下列问题:

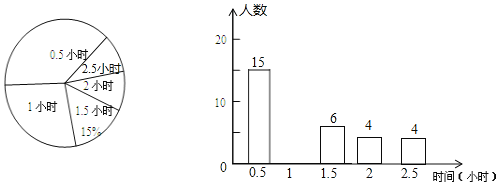
    (1)本次调查抽取的老年人共有多少名?将条形图补充完整;

    (2)被调查的老年人中参加文体活动的中位数是多少?

    (3)请估计该街道参加文体活动的老年人中,大约有多少人平均每天参加文体活动的时间不少于1小时?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一直角坐标系中，一次函数y=ax+c和二次函数y=a（x+c）2的图象大致为（　　）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案