
分析 先利用坐标轴上点的坐标特征求出A点和B点坐标,然后利用网格特征和旋转的性质求出△AOB绕点B顺时针或逆时针旋转90°后A的对应点C的坐标.
解答 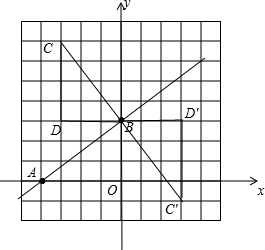 解:当x=0时,$\frac{3}{4}$x+3=0,解得x=-4,则A(4,0),
解:当x=0时,$\frac{3}{4}$x+3=0,解得x=-4,则A(4,0),
当y=0时,y=$\frac{3}{4}$x+3=3,则B(0,3),
如图,当△AOB绕点B顺时针旋转90°得到△CDB,C点坐标为(-3,7),
当△AOB绕点B顺时针旋转90°得到△C′D′B,C′点坐标为(3,-1).
故答案为(-3,7)或(3,-1).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
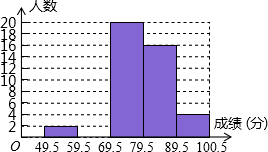 某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必有一根为$\frac{1}{3}$ | B. | 必有一根为$\frac{1}{9}$ | ||
| C. | 两根分别为$\frac{1}{3}$,-$\frac{1}{3}$ | D. | 必有一根为$\frac{1}{3}$或-$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2是不等式x-3<8的解 | B. | -4不是不等式$\frac{1}{2}$x+2>0的解 | ||
| C. | -1是不等x≥-2的解 | D. | 不等式x>0和x≥0的解集相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请解答问题:
请解答问题:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com