
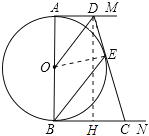
【题目】已知:如图, AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD , 作BE∥OD交⊙O于点E, 联结DE并延长交BN于点C.
(1)求证:DC是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.

【答案】(1)证明见解析;(2)4.
【解析】
试题(1)连接OE,由OE=OB,利用等边对等角得到一对角相等,再由OD与BE平行,得到一对同位角及一对内错角相等,等量代换得到∠AOD=∠OBE=∠OEB=∠EOD,再由OA=OE,OD=OD,利用SAS得到三角形AOD与三角形EOD全等,由全等三角形对应角相等得到∠OAD=∠OED,根据AM为圆O的切线,利用切线的性质得到∠OAD=∠OED=90°,即可得证.
(2)过点D作BC的垂线,垂足为H,由BN与圆O切线于点B,得到∠ABC=90°=∠BAD=∠BHD,利用三个角为直角的四边形为矩形得到ADHB为矩形,利用矩形的对边相等得到BH=AD=1,AB=DH,由BC-BH求出HC的长,AD、CB、CD分别切⊙O于点A、B、E,利用切线长定理得到AD=DE=1,EC=BC=4,在直角三角形DHC中,利用勾股定理求出DH的长,即为AB的长.
试题解析:(1)如图,连接OE,
在⊙O中,OA=OE=OB,∴∠OBE=∠OEB.
∵OD∥BE,∴∠AOD=∠OBE=∠OEB=∠EOD.
在△AOD和△EOD中,OA=OE,∠AOD=∠EOD,OD=OD,
∴△AOD≌△EOD(SAS).∴∠OAD=∠OED.
∵AM是⊙O的切线,切点为A,∴BA⊥AM.
∴∠OAD=∠OED=90°.∴OE⊥DE.
∵OE是⊙O的半径,∴DE是⊙O的切线.
(2)如图,过点D作BC的垂线,垂足为H,
∵BN切⊙O于点B,∴∠ABC=90°=∠BAD=∠BHD.∴四边形ABHD是矩形.
∴AD=BH=1,AB=DH,∴CH=BC-BH=4-1=3.
∵AD、CB、CD分别切⊙O于点A、B、E,∴AD=ED=1,BC=CE=4.
∴DC=DE+CE=1+4=5,
在Rt△DHC中,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,点D是线段AB上的动点,M、N分别是AD、CD的中点,连接MN,当点D由点A向点B运动的过程中,线段MN所扫过的区域的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
折纸,常常能为证明一个命题提供思路和方法.例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?


把AC沿∠A的角平分线AD翻折,因为AB>AC,所以点C落在AB上的点![]() 处,即
处,即![]() ,据以上操作,易证明
,据以上操作,易证明![]() ≌
≌![]() ,所以
,所以![]() ,又因为
,又因为![]() >∠B,所以∠C>∠B.
>∠B,所以∠C>∠B.
感悟与应用:
(1)如图(a),在△ABC中,∠ACB=90°,∠B=30°,CD平分∠ACB,试判断AC和AD、BC之间的数量关系,并说明理由;
(2)如图(b),在四边形ABCD中,AC平分∠BAD,AC=16,AD=8,DC=BC=12,
① 求证:∠B+∠D=180°;
② 求AB的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xoy中,直线y=![]() x+
x+![]() 交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).
交x轴于点B,交y轴于点A,过点C(1,0)作x轴的垂线l,将直线l绕点C按逆时针方向旋转,旋转角为α(0°<α<180°).

(1)当直线l与直线y=![]() x+
x+![]() 平行时,求出直线l的解析式;
平行时,求出直线l的解析式;
(2)若直线l经过点A,①求线段AC的长;②直接写出旋转角α的度数;
(3)若直线l在旋转过程中与y轴交于D点,当△ABD、△ACD、△BCD均为等腰三角形时,直接写出符合条件的旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题:

(l)利用树状图(或列表)的方法表示游戏所有可能出现的结果;
(2)求甲、乙两人获胜的概率,并说明游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
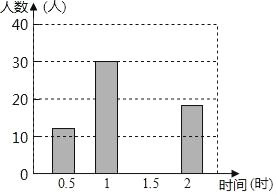
【题目】某校倡议八年级学生利用双休日在各自社区参加义务劳动.为了了解同学们参加义务劳动的时间,学校随机调查了部分同学参加义务劳动的时间,用得到的数据绘制成如下不完整的统计图表:
劳动时间(时) | 频数(人) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合计 | m | 1 |
(1)统计表中的m=_____,x=______,y=_______;
(2)请将频数分布直方图补充完整;
(3)求被调查同学的平均劳动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC为等腰直角三角形, △ABD为等边三角形,连接CD.
(1)求∠ACD的度数;
(2)如图①,作∠BAC的平分线交CD于点E,求证:DE=AE+CE;
(3)如图②,在(2)的条件下,M为线段BC右侧一点,满足∠CMB=60°,求证:ME平分∠CMB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系。
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;



(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系? (不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。

![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com