Question

12．如图，一边长为2的正方形ABCD的对角线AC所在的射线AQ上有一动点Q，射线OP⊥AQ．设CO=x，∠POQ与正方形公共部分的面积为S．
（1）求S与x之间的函数关系式；
（2）当OP平分AD边时求出S的值．

Answer 1

分析 （1）根据正方形的性质得到∠DCA=45°，由∠POC=90°，即可得到结论；
（2）OP平分AD边时，如图，根据正方形的性质得到∠DAC=45°，推出△AOG是等腰直角三角形，解直角三角形得到AO=OG=$\frac{\sqrt{2}}{2}$，即可得到结论．

解答 解：（1）∵四边形ABCD是正方形，
∴∠DCA=45°，
∵∠POC=90°，
∴S=$\frac{1}{2}O{C}^{2}$=$\frac{1}{2}$x²；

（2）OP平分AD边时，如图，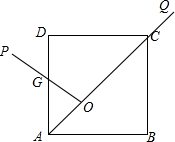
∵四边形ABCD是正方形，
∴∠DAC=45°，
∴△AOG是等腰直角三角形，
∵AG=$\frac{1}{2}$AD=1，
∴AO=OG=$\frac{\sqrt{2}}{2}$，
∴S=$\frac{1}{2}$×（$\frac{\sqrt{2}}{2}$）²=$\frac{1}{4}$．

点评 本题考查了根据三角形的面积公式求函数关系式，正方形的性质，等腰直角三角形的性质，熟练掌握辅助线的性质是解题的关键．