
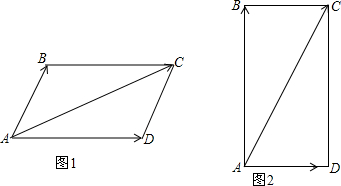
分析 此题实际上是求AC的长度和∠DAC的大小.通过解直角△ADC可以求得∠DAC的度数,根据$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$来求$\overrightarrow{AC}$.
解答 解:依题意得:AD=2,DC=AB=2$\sqrt{3}$,∠ADC=90°.
∵在直角△ADC中,tan∠∠DAC=$\frac{CD}{AD}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠DAC=60°,
又∵$\overrightarrow{AD}$=2,$\overrightarrow{AB}$=2$\sqrt{3}$,
∴|$\overrightarrow{AC}$|=|$\overrightarrow{AB}$+$\overrightarrow{AD}$|=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4.
答:小明爸爸游到对岸的实际速度是4km/h,方向与河岸成60°夹角.
点评 本题考查了平面向量.理解平行四边形法则是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:解答题
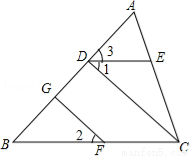
∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
函数y=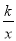 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com