
【题目】如图,抛物线y=a(x+3)(x﹣k)交x轴于点A、B,(A左B右),交y轴于点C,△AOC的周长为12,sin∠CBA=![]() ,则下列结论:①A点坐标(﹣3,0);②a=﹣
,则下列结论:①A点坐标(﹣3,0);②a=﹣![]() ;③点B坐标(8,0);④对称轴x=
;③点B坐标(8,0);④对称轴x=![]() .其中正确的有( )个.
.其中正确的有( )个.
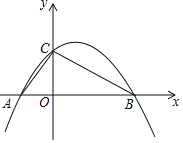
A.4B.3C.2D.1
【答案】A
【解析】
令y=0,求得A点坐标,B点用字母k表示的坐标,再把抛物线的解析式化成一般形式,则可用a与k的代数式表示OC,进而根据sin∠CBA=![]() ,用a与k的代数式表示BC,在由勾股定理得出a与k的方程,求得a的值,再根据△AOC的周长为12,求得k的值,则题目中的问题便可解决.
,用a与k的代数式表示BC,在由勾股定理得出a与k的方程,求得a的值,再根据△AOC的周长为12,求得k的值,则题目中的问题便可解决.
令y=0,则y=a(x+3)(x﹣k)=0,
解得x=﹣3或k,
∴A(﹣3,0),B(k,0),
故①正确;
∵y=a(x+3)(x﹣k)=ax2+(3a﹣ak)x﹣3ak,
∴C(0,﹣3ak),
∴OC=﹣3ak,
∵sin∠CBA=![]() ,
,
∴![]() ,
,
∴BC=![]() ,
,
∵BC2﹣OC2=OB2,
∴45a2k2﹣9a2k2=k2,
∴a2=![]() ,
,
∵抛物线的开口向下,
∴a=﹣![]() ,
,
故②正确;
∴OC=![]() k,
k,
∴AC=![]() ,
,
∵△AOC的周长为12,
∴3+![]() k+
k+![]() =12,
=12,
解得,k=8,
∴B(8,0),
故③正确;
∵A(﹣3,0),B(8,0),
∴对称轴为:x=![]() ,
,
故④正确.
综上所述①②③④都正确
故选:A.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() 交坐标轴于A、C两点,抛物线
交坐标轴于A、C两点,抛物线![]() 过A、C两点.
过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家住重庆两相邻小区的小明和小华在一次数学课后,进行了一次数学实践活动.如图,在同一水平面从左往右依次是小明家所在的居民楼、小华家所在的小洋房、背靠小华家的一座小山,实践内容为测量小山的高度,家住顶楼的小明在窗户A处测得小山山顶的一棵大树顶端E的俯角为10°,小华在自家楼下C处测得小明家窗户A处的仰角为37°,且测得坡面CD的坡度i=1:2,已知两家水平距离BC=120米,大树高度DE=3米,则小山山顶D到水平面BF的垂直高度约为( )(精确到0.1米,参考数据sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin10°≈
,sin10°≈![]() ,tan10°≈
,tan10°≈![]() )
)

A.55.0米B.50.3米C.48.1 米D.57.3米
查看答案和解析>>
科目:初中数学 来源: 题型:
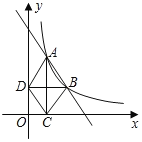
【题目】如图,在直角坐标平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
(1)求反比例函数的解析式;
(2)若△ABD的面积为4,求点B的坐标;
(3)求证:DC![]() AB.
AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
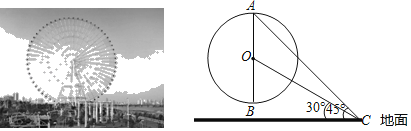
【题目】“天空之城”摩天轮,位于宁波市杭州湾新区欢乐世界.摩天轮高约126米(最高点到地面的距离).如图,点O是摩天轮的圆心,AB是其垂直于地面的直径,小明在地面C处用测角仪测得摩天轮最高点A的仰角为45°,测得圆心O的仰角为30°,求摩天轮的半径.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣![]() x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.
x2+bx+c(b,c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C.

(1)求该抛物线的解析式;
(2)P是抛物线上一动点(不与点A、B重合),
①如图2,若点P在直线AB上方,连接OP交AB于点D,求![]() 的最大值;
的最大值;
②如图3,若点P在x轴的上方,连接PC,以PC为边作正方形CPEF,随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
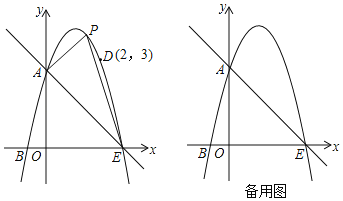
【题目】如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E,点P为直线AE上方抛物线上一动点,设点P的横坐标为t.
(1)求抛物线的表达式;
(2)当t为何值时,△PAE的面积最大?并求出最大面积;
(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com