
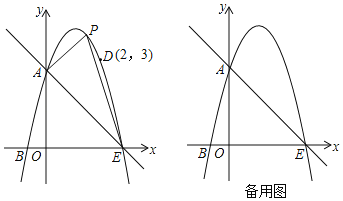
【题目】如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E,点P为直线AE上方抛物线上一动点,设点P的横坐标为t.
(1)求抛物线的表达式;
(2)当t为何值时,△PAE的面积最大?并求出最大面积;
(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3;(2)t=![]() 时,△PAE的面积最大,最大值是
时,△PAE的面积最大,最大值是![]() ;(3)t的值为1或
;(3)t的值为1或![]() .
.
【解析】
(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)由抛物线的对称性可求得E点坐标,从而可求得直线EA的解析式,作PM∥y轴,交直线AE于点M,则可用t表示出PM的长,从而可表示出△PAE的面积,再利用二次函数的性质可求得其最大值即可;
(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.
解:(1)由题意得: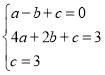 ,
,
解得: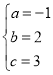 ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(0,3),D(2,3),
∴抛物线对称轴为x=1,
∴E(3,0),
设直线AE的解析式为y=kx+3,
∴3k+3=0,解得,k=﹣1,
∴直线AE的解析式为y=﹣x+3,
如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),
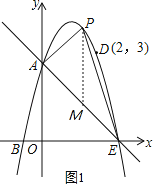
∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,
∴![]() =
=![]() =
=![]() ,
,
∴t=![]() 时,△PAE的面积最大,最大值是
时,△PAE的面积最大,最大值是![]() .
.
(3)由图可知∠PEA≠90°,
∴只能有∠PAE=90°或∠APE=90°,
①当∠PAE=90°时,如图2,作PG⊥y轴,

∵OA=OE,
∴∠OAE=∠OEA=45°,
∴∠PAG=∠APG=45°,
∴PG=AG,
∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),
②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,
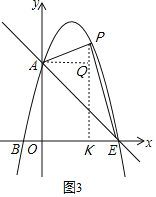
则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,
∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,
∴∠PAQ=∠KPE,且∠PKE=∠PQA,
∴△PKE∽△AQP,
∴![]() ,
,
∴![]() ,
,
即t2﹣t﹣1=0,解得:t=![]() 或t=
或t=![]() <0(舍去),
<0(舍去),
综上可知存在满足条件的点P,t的值为1或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x+3)(x﹣k)交x轴于点A、B,(A左B右),交y轴于点C,△AOC的周长为12,sin∠CBA=![]() ,则下列结论:①A点坐标(﹣3,0);②a=﹣
,则下列结论:①A点坐标(﹣3,0);②a=﹣![]() ;③点B坐标(8,0);④对称轴x=
;③点B坐标(8,0);④对称轴x=![]() .其中正确的有( )个.
.其中正确的有( )个.
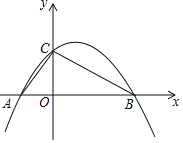
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
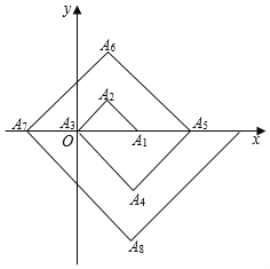
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为更好地提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买![]() 个温馨提示牌和
个温馨提示牌和![]() 个垃圾箱共需
个垃圾箱共需![]() 元,且每个温馨提示牌比垃圾箱便宜
元,且每个温馨提示牌比垃圾箱便宜![]() 元.
元.
(1)问购买![]() 个温馨提示牌和
个温馨提示牌和![]() 个垃圾箱各需多少元?
个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共![]() 个费用不超过
个费用不超过![]() 元,求最多购买垃圾箱多少个.
元,求最多购买垃圾箱多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
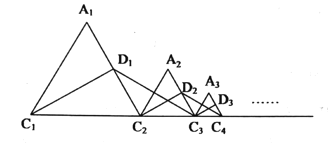
【题目】如图,等边![]() 的周长为1,作
的周长为1,作![]() 于
于![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() ;作
;作![]() 于
于![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() ;…且点
;…且点![]() ,
,![]() ,
,![]() ,…都在直线
,…都在直线![]() 同侧,如此下去,可得到
同侧,如此下去,可得到![]() 的边长为__________.(
的边长为__________.(![]() ,且
,且![]() 为整数)
为整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |
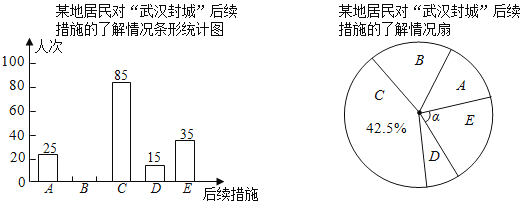
已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,以点
,以点![]() 为直角项点,
为直角项点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() ,分别交直线
,分别交直线![]() 和
和![]() 轴于
轴于![]() ,
,![]() 两点,以点
两点,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,…,按此规律进行下去,则点
,…,按此规律进行下去,则点![]() 的坐标为__________ (结果用含正整数
的坐标为__________ (结果用含正整数![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
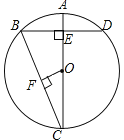
A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com