
【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |
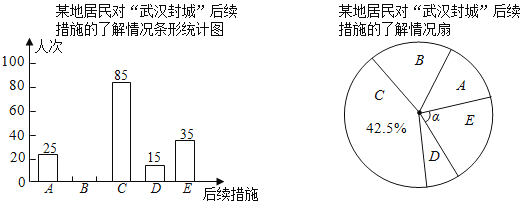
已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.
【答案】(1)100,图详见解析;(2)63°;(3)约为15万人.
【解析】
(1)由题意根据条形图和扇形图的数据计算,求出总选择人次,根据平均每人恰好选择了两个选项,求出参与本次问卷调查的居民人数;
(2)根据题意求出B类选择人次,补全条形统计图;
(3)根据题意求出选择D选项的人数的百分比,用样本估计总体即可.
解:(1)由条形图可知,C类人次为85人,由扇形图可知,C类人次所占的百分比为42.5%,
∴总选择人次为:85÷42.5%=200(人),
∵平均每人恰好选择了两个选项,
∴参与本次问卷调查的居民人数为100人,
B类选择人次为:200﹣25﹣85﹣15﹣35=40,则补全条形统计图如图所示;
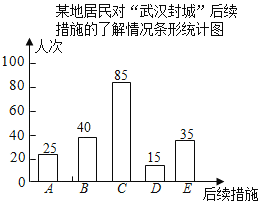
(2)E选项对应圆心角α=![]() ×360°=63°;
×360°=63°;
(3)该地100万居民当中选择D选项的人数=100×![]() =15(万人),
=15(万人),
答:该地100万居民当中选择D选项的人数约为15万人.


科目:初中数学 来源: 题型:
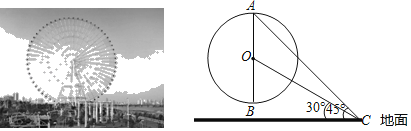
【题目】“天空之城”摩天轮,位于宁波市杭州湾新区欢乐世界.摩天轮高约126米(最高点到地面的距离).如图,点O是摩天轮的圆心,AB是其垂直于地面的直径,小明在地面C处用测角仪测得摩天轮最高点A的仰角为45°,测得圆心O的仰角为30°,求摩天轮的半径.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是![]() 的直径,点P在BA的延长线上,PD切
的直径,点P在BA的延长线上,PD切![]() 于点D,过点B作
于点D,过点B作![]() ,交PD的延长线于点C,连接AD并延长,交BE于点E.
,交PD的延长线于点C,连接AD并延长,交BE于点E.
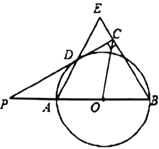
(Ⅰ)求证:AB=BE;
(Ⅱ)连结OC,如果PD=2![]() ,∠ABC=60°,求OC的长.
,∠ABC=60°,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
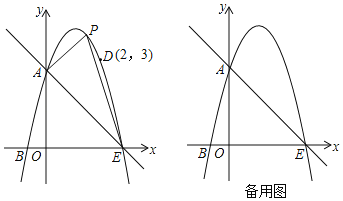
【题目】如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E,点P为直线AE上方抛物线上一动点,设点P的横坐标为t.
(1)求抛物线的表达式;
(2)当t为何值时,△PAE的面积最大?并求出最大面积;
(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
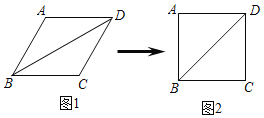
【题目】小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,接着活动学具成为图2所示,并测得∠ABC=90°,若图2对角线BD=40cm,则图1中对角线BD的长为( )
A.20cmB.20![]() cmC.20
cmC.20![]() cmD.20
cmD.20![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
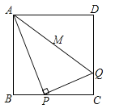
【题目】正方形ABCD的边长为4,P 为BC上的动点,连接PA,作PQ⊥PA,PQ交CD于Q,连接AQ ,则AQ的最小值是( )
A.5B.![]() C.
C.![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售,经市场调查发现,草莓销售不会亏本,且每天的销售量y(千克)与销售单价x(元/千克)之间函数关系如图所示.

(1)求y与x的函数关系式,并写出x的取值范围.
(2)当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?
(3)某村今年草莓采摘期限30天,预计产量6000千克,则按照(2)中的方式进行销售,能否销售完这批草莓?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
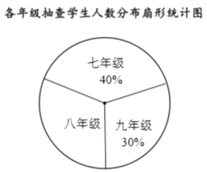
【题目】某初中为了了解学生的视力情况,从三个年级随机抽取了部分学生进行调查,并制作了下面的统计表和统计图.
各年级抽查学生视力各等第人数分布统计表
优秀 | 良好 | 合格 | 不合格 | |
七年级 |
| 20 | 22 | 23 |
八年级 | 11 | 17 | 13 | 19 |
九年级 | 8 |
| 11 | 25 |
(1)在统计表中,![]() ________,
________,![]() ________;
________;
(2)在扇形统计图中,八年级所对应的扇形圆心角为________°;
(3)若该校三个年级共有1800名学生,试估计该校学生视力等第不合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
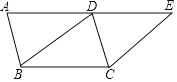
【题目】如图,四边形ABCD是平行四边形,延长AD至点E,使DE=AD,连接BD.
(1)求证:四边形BCED是平行四边形;
(2)若DA=DB=2,cosA=![]() ,求点B到点E的距离.
,求点B到点E的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com