练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

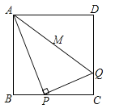
    【题目】正方形ABCD的边长为4，P 为BC上的动点，连接PA，作PQ⊥PA，PQ交CD于Q，连接AQ ，则AQ的最小值是（ ）

    A.5B.C.D.4

    【答案】A

    【解析】

    设BP=x，CQ=y，根据△ABP∽△PCQ可得y关于x的二次函数，利用二次函数的性质，求得y的最大值情况，则QD最小，则AQ最小．

    ∵四边形ABCD是正方形，

    ∴∠B＝∠C＝90°，

    ∵PQ⊥AP，

    ∴∠APB+∠QPC＝90°，

    ∠APB+∠BAP＝90°，

    ∴∠BAP＝∠QPC，

    ∴△ABP∽△PCQ，

    ∴，

    设BP=x，CQ=y

    即，

    ∴y＝﹣+x＝﹣+1(0＜x＜4)，

    ∵﹣＜0，

    ∴y有最大值，

    ∴当x＝2时，y有最大值1cm．此时QD=3

    在Rt△AQP中，

    故AQ的最小值是5

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一般地，对于已知一次函数y1=ax+b，y2=cx+d（其中a，b，c，d为常数，且ac＜0），定义一个新函数y=，称y是y1与y2的算术中项，y是x的算术中项函数．

    （1）如：一次函数y1=x﹣4，y2=﹣x+6，y是x的算术中项函数，即y=．

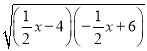    ①自变量x的取值范围是　 　，当x=　 　时，y有最大值；

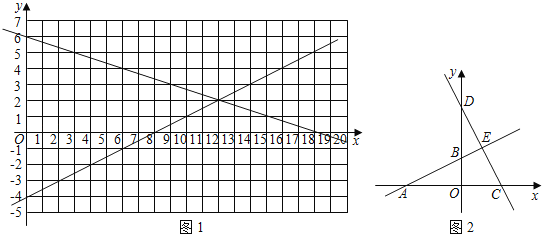
    ②根据函数研究的途径与方法，请填写下表，并在图1中描点、连线，画出此函数的大致图象；

    x

    8

    9

    10

    12

    13

    14

    16

    17

    18

    y

    0

    1.2

    1.6

    　 　

    2.04

    2

    　 　

    1.2

    0

    ③请写出一条此函数可能有的性质　 　；

    （2）如图2，已知一次函数y1=x+2，y2=﹣2x+6的图象交于点E，两个函数分别与x轴交于点A，C，与y轴交于点B，D，y是x的算术中项函数，即y=．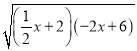

    ①判断：点A、C、E是否在此算术中项函数的图象上；

    ②在平面直角坐标系中是否存在一点，到此算术中项函数图象上所有点的距离相等，如果存在，请求出这个点；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小区为更好地提高业主垃圾分类的意识，管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱，若购买个温馨提示牌和个垃圾箱共需元，且每个温馨提示牌比垃圾箱便宜元．

    （1）问购买个温馨提示牌和个垃圾箱各需多少元？

    （2）如果需要购买温馨提示牌和垃圾箱共个费用不超过元，求最多购买垃圾箱多少个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的直径AB＝26，P是AB上(不与点A、B重合)的任一点，点C、D为⊙O上的两点，若∠APD＝∠BPC，则称∠CPD为直径AB的“回旋角”．

    (1)若∠BPC＝∠DPC＝60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；

    (2)若的长为π，求“回旋角”∠CPD的度数；

    (3)若直径AB的“回旋角”为120°，且△PCD的周长为24+13，直接写出AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校兴趣小组以问卷调查的形式，随机调查了某地居民对武汉封城后续措施的了解情况，设置了多选题，并将调查结果绘制成如图不完整的统计图．

    选项

    A

    B

    C

    D

    E

    后续措施

    扩大宣传力度

    分类隔离病人

    封闭小区

    聘请专业物资

    采取其他措施

    选择人次

    25

    85

    15

    35

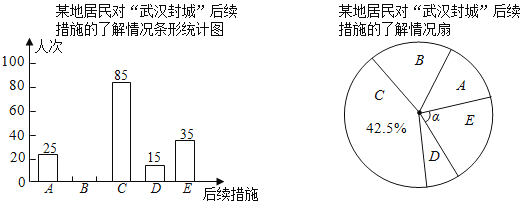
    已知平均每人恰好选择了两个选项，根据以上信息回答下列问题：

    （1）求参与本次问卷调查的居民人数，并补全条形统计图；

    （2）在扇形统计图中，求E选项对应圆心角α的度数；

    （3）根据此次调查结果估计该地100万居民当中选择D选项的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OF⊥AB，交AC于点F，点E在AB的延长线上，射线EM经过点C，且∠ACE+∠AFO＝180°．

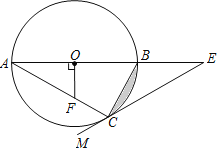
    （1）求证：EM是⊙O的切线；

    （2）若∠A＝∠E，⊙O的半径为1，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点在直线上，过点作轴交轴于点，以点为直角项点，为直角边在的右侧作等腰直角，再过点作，分别交直线和轴于，两点，以点为直角顶点，为直角边在的右侧作等腰直角，…，按此规律进行下去，则点的坐标为__________ (结果用含正整数的代数式表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    …

    y

    …

    0

    4

    6

    6

    4

    …

    从上表可知，下列说法中，错误的是（ ）

    A. 抛物线于x轴的一个交点坐标为（﹣2，0）

    B. 抛物线与y轴的交点坐标为（0，6）

    C. 抛物线的对称轴是直线x=0

    D. 抛物线在对称轴左侧部分是上升的

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC绕点A逆时针旋转得到△ADE，其中点B、C分别与点D、E对应，如果B、D、C三点恰好在同一直线上，那么下列结论错误的是（ ）

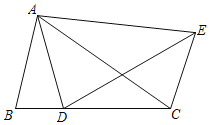
    A.∠ACB＝∠AEDB.∠BAD＝∠CAE

    C.∠ADE＝∠ACED.∠DAC＝∠CDE

    查看答案和解析>>

    同步练习册答案