
【题目】已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则下列结论:①△ABE的面积为6cm2,②BF的长为5cm,③EF的长为![]() cm,④四边形CDEF的面积是13.5cm2.其中正确的个数有( )
cm,④四边形CDEF的面积是13.5cm2.其中正确的个数有( )
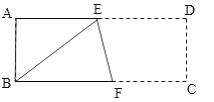
A.4B.3C.2D.1
【答案】A
【解析】
①由勾股定理构造方程可求得AE,则△ABE的面积可求;②由折叠及平行线性质,可证明BD=BE,则问题可解;③过点E作ED⊥BC于H,利用勾股定理求EF;④由①、②,可求得ED、FC,则四边形CDEF的面积可求;
解:①由折叠可知,BE=DE
∵AD=9
∴BE=9-AE
RtΔABE中,
AB2+AE2=BE2
∴32+AE2=(9-AE)2
∴AE=4
∴△ABE的面积为![]()
∴△ABE的面积为6cm2
故①正确;
②由①DE=BE=5
由折叠可知, ∠BEF=∠DEF
∵AD∥BC
∴∠BFE=∠DEF
∴∠BFE=∠BEF
∴BF=BE=5
故BF的长为5cm
②正确;
③过点E作ED⊥BC于H
由①、②可知,HF=1,EH=AB=3
则Rt△EHF中:
EF=![]()
则EF的长为![]() cm
cm
③正确;
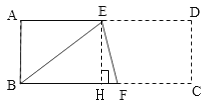
④由①、②可知,ED=5,FC=BC-BF=4
∴四边形CDEF的面积:![]()
四边形CDEF的面积是13.5cm2.
④正确;
故应选A


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为4的等边△ABC中.
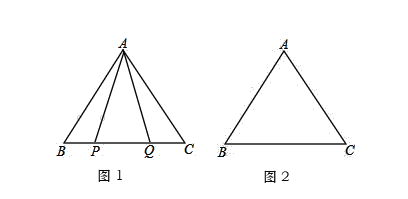
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=18°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.依题意将图2补全,并求证PA=PM.
(3)在(2)中,当AM的值最小时,直接写出CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
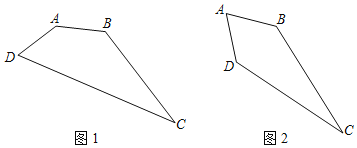
【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.如图1是一个四边形的木架,AB=AD=2cm,BC=5cm.
(1)扭动这个木架,四边形的形状就会改变,这说明了什么?
(2)如图2,若固定三根木条AB、BC、AD不动,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(3)在扭动这个木架过程中,当测得A、C之间的距离为6cm时,若CD的长度也是整数,那么CD的长应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为2、3、4,正放置的四个正方形的面积分别为S1,S2,S3,S4,则S1+S2+S3+S4=______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的部分图象如图所示,则下列结论:
①abc>0;②3a+c=0;③当y>0时,﹣3<x<1;④b2>4ac;⑤当y=3时,x只能等于0.
其中正确结论的个数为( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:OF∥BC;
(2)求证:△AFO≌△CEB;
(3)若EB=5cm,CD=![]() cm,设OE=x,求x值及阴影部分的面积
cm,设OE=x,求x值及阴影部分的面积

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com