
【题目】在边长为4的等边△ABC中.
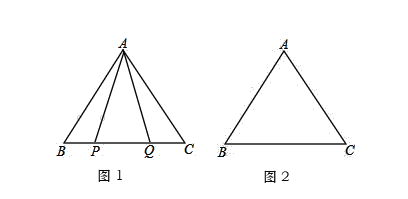
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=18°,求∠AQB的度数;
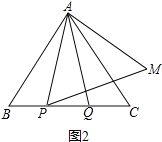
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.依题意将图2补全,并求证PA=PM.
(3)在(2)中,当AM的值最小时,直接写出CM的长.
【答案】(1)78°;(2)见解析;(3)2.
【解析】
(1)根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,根据三角形外角的性质即可得到结论;
(2)如图2根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.
(3)因为AM=AP,所以当AP⊥BC时,AM的值最小,此时P、Q重合,由此即可解决问题;
(1)∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
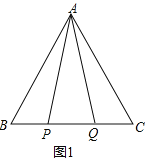
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ=18°,
∴∠AQB=∠APQ=∠BAP+∠B=78°;
(2)如图2,∵点Q关于直线AC的对称点为M,
∴AQ=AM,∠QAC=∠MAC,
∵∠BAP=∠CAQ,
∴∠MAC=∠BAP,
∴∠BAP+∠PAC=∠MAC+∠CAP=60°,
∴∠PAM=60°,
∵AP=AQ,
∴AP=AM,
∴△APM是等边三角形,
∴AP=PM.
(3)∵AM=AP,
∴当AP⊥BC时,AM的值最小,
∴此时P、Q重合,CM=CQ=QB=2.


科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两山地自行车选手进行骑行训练.他们在同地出发,反向而行,分别前往A地和B地.甲先出发一分钟且先到达A地.两人到达目的地后均以原速按原路立即返回,直至两人相遇.下图是两人之间的距离y(千米)随乙出发时间x(分钟)之间的变化图象.请根据图象解决下列问题:
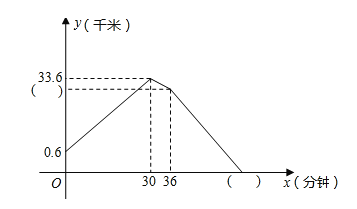
(1)直接写出甲车和乙车的速度.
(2)在图中的两个括号内填上正确的数值.
(3)乙车出发多长时间两车首次相距22.6千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,延长AC到E,C为线段AE上的一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC. 以下五个结论:①AD=BE;②AP=BO;③PQ//AE;④∠AOB=60°;⑤OC平分∠AOE;结论正确的有_________(把你认为正确的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段圆弧与长度为![]() 的正方形网格的交点是A、B、C.
的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;

(2)请在(1)的基础上,完成下列填空:
①⊙D的半径![]() (结果保留根号).
(结果保留根号).
②点(-2,0)在⊙D ;(填“上”、“内”、“外”)
③∠ADC的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则下列结论:①△ABE的面积为6cm2,②BF的长为5cm,③EF的长为![]() cm,④四边形CDEF的面积是13.5cm2.其中正确的个数有( )
cm,④四边形CDEF的面积是13.5cm2.其中正确的个数有( )
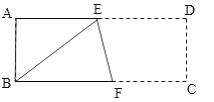
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=![]() x2﹣
x2﹣![]() (m﹣1)x﹣
(m﹣1)x﹣![]() m(m>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.
m(m>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.
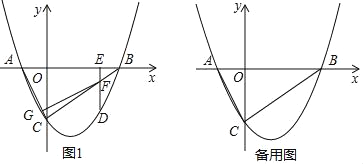
(1)求该抛物线的函数表达式;
(2)动点D在线段BC下方的抛物线上.
①连接AC、BC,过点D作x轴的垂线,垂足为E,交BC于点F.过点F作FG⊥AC,垂足为G.设点D的横坐标为t,线段FG的长为d,用含t的代数式表示d;
②过点D作DH⊥BC,垂足为H,连接CD.是否存在点D,使得△CDH中的一个角恰好等于∠ABC的2倍?如果存在,求出点D的横坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com