
已知二次函数y = ax2的图象经过点(2,1).
(1)求二次函数y = ax2的解析式;
(2)一次函数y = mx+4的图象与二次函数y = ax2的图象交于A(x1、y1)、B(x2、y2)两点.
①当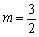 时(图①),求证:△AOB为直角三角形;
时(图①),求证:△AOB为直角三角形;
②试判断当 时(图②),△AOB的形状,并证明;
时(图②),△AOB的形状,并证明;
(3)根据第(2)问,说出一条你能得到的结论.(不要求证明)
 |
解:(1)由条件得1 = 4a,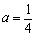 ,所以二次函数的解析式是
,所以二次函数的解析式是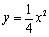 …………………1分
…………………1分
 (2)①由
(2)①由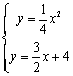 得
得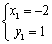 ,
,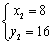 ,
,
即A(-2,1),B(8,16)…………………………3分
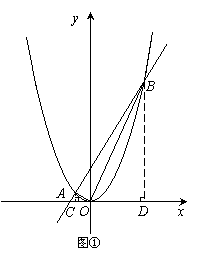
过A作AC⊥x轴于C,过B作BD⊥x轴于D,
则AC = 1,OC = 2,OD = 8,BD = 16,
∴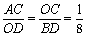 又∵∠ACO =∠ODB = 90º
又∵∠ACO =∠ODB = 90º
∴△ACO ∽ △ODB ………………………………4分
∴∠AOC = ∠OBD
∴∠AOC +∠BOD = 90º
∴∠AOB = 90º
∴△AO B为直角三角形 …………………………………………………………
B为直角三角形 …………………………………………………………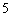 分
分
②△AOB为直角三角形, ………………………………………………………………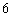 分
分
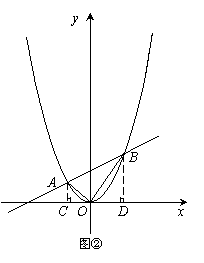 证明如下:
证明如下:
过A作AC⊥x轴于C,过B作BD⊥x轴于D
由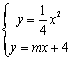 得x2-4mx-16 = 0
得x2-4mx-16 = 0
解得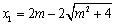 ,
, …………
…………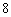 分
分
∴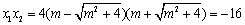
∴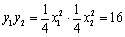 …………
………… …………………
…………………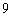 分
分
∴OC•OD = AC•BD = 16
∴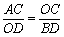 …………………………………………
………………………………………… ……………………………
……………………………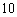 分
分
又∵∠ACO =∠ODB = 90º,∴△ACO ∽△ODB ………………………………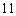 分
分
∴∠AOC =∠OBD
∴∠AOC +∠BOD =90º ∴∠AOB =90º
∴△AOB为直角三角形.
(3)可能的结论为 …………………………………………………………………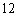 分
分
如果过定点(0,4)的直线与抛物线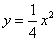 交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.
交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.
如果过定点(0, )的直线与抛物线
)的直线与抛物线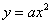 交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.
交于A、B两点,O为抛物线的顶点,那么△AOB必为直角三角形.


科目:初中数学 来源: 题型:
已知一次函数
 的图像与
的图像与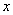 轴、
轴、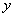 轴分别相交于点A、B,点P在该函数图像上, P到
轴分别相交于点A、B,点P在该函数图像上, P到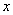 轴、
轴、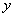 轴的距离分别为
轴的距离分别为 、
、 。
。
(1)当P为线段AB的中点时,求 的值;
的值;
(2)直接写出 的范围,并求当
的范围,并求当 时点P的坐标;
时点P的坐标;
(3)若在线段AB 上存在无数个P点,使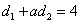 (
(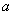 为常数), 求
为常数), 求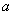 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练.球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传球三次.
(1)请利用树状图列举出三次传球的所有可能情况;
(2)求三次传球后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知四边形ABCD,下列说法正确的是
A.当AD=BC,AB//DC时,四边形ABCD是平行四边形
B.当AD=BC,AB=DC时,四边形ABCD是平行四边形
C.当AC=BD,AC平分BD时,四边形ABCD是矩形
D.当AC=BD,AC⊥BD时,四边形ABCD是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com