
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
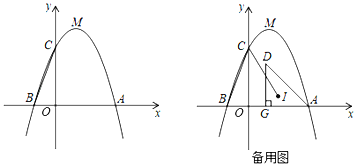
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG⊥x轴于点G,设△ADG的内心为I,试求CI的最小值.
【答案】(1)y=﹣x2+2x+3;(2)存在,点P坐标为(0,﹣![]() )或(0,1)或(0,3)或(0,
)或(0,1)或(0,3)或(0,![]() ),理由见解析;(3)
),理由见解析;(3)![]()
【解析】
(1)将A(3,0),B(﹣1,0)两点的坐标代入y=ax2+bx+3即可求得答案;
(2)设点P坐标为(0,p),可求得顶点M(1,4),利用两点之间的距离公式分别求得![]() 、
、![]() 、
、![]() ,分类讨论计算:当∠PAM=90°、∠APM=90°、∠AMP=90°时p的值,从而得到结论;
,分类讨论计算:当∠PAM=90°、∠APM=90°、∠AMP=90°时p的值,从而得到结论;
(3)根据三角形内心的定义作三边的高线,根据三角形内心的性质知四边形IEGH是正方形,设点I坐标为(m,n),根据点的坐标的意义及切线长定理求得:AG=n+3﹣m,DG=m+n,由勾股定理DG2+AG2=DA2化简并配方得:(m﹣![]() )2+(n+
)2+(n+![]() )2=
)2=![]() ,逆用两点之间的距离公式知:点I(m,n)与定点Q(
,逆用两点之间的距离公式知:点I(m,n)与定点Q(![]() ,﹣
,﹣![]() )的距离为
)的距离为![]() ,当点I在线段CQ上时,CI最小,从而求得答案.
,当点I在线段CQ上时,CI最小,从而求得答案.
解:(1)∵抛物线y=ax2+bx+3过点A(3,0),B(﹣1,0)
∴![]() , 解得:
, 解得:![]() .
.
∴这条抛物线对应的函数表达式为y=﹣x2+2x+3.
(2)在y轴上存在点P,使得△PAM为直角三角形.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点M(1,4),
∴AM2=(3﹣1)2+42=20,
设点P坐标为(0,p),
①AP2=32+p2=9+p2,MP2=12+(4﹣p)2=17﹣8p+p2/span>
若∠PAM=90°,则AM2+AP2=MP2,
∴20+9+p2=17﹣8p+p2,解得:p=﹣![]() ,
,
∴P(0,﹣![]() );
);
②若∠APM=90°,则AP2+MP2=AM2,
∴9+p2+17﹣8p+p2=20,解得:p1=1,p2=3,
∴P(0,1)或(0,3);
③若∠AMP=90°,则AM2+MP2=AP2,
∴20+17﹣8p+p2=9+p2,解得:p=![]() ,
,
∴P(0,![]() )
)
综上所述,点P坐标为(0,﹣![]() )或(0,1)或(0,3)或(0,
)或(0,1)或(0,3)或(0,![]() )时,△PAM为
)时,△PAM为
直角三角形.
(3)如图,过点I作IE⊥x轴于点E,IF⊥AD于点F,IH⊥DG于点H
∵DG⊥x轴于点G,∴∠HGE=∠IEG=∠IHG=90°,∴四边形IEGH是矩形,
∵点I为△ADG的内心,∴IE=IF=IH,AE=AF,DF=DH,EG=HG,
∴矩形IEGH是正方形,
设点I坐标为(m,n),
∴OE=m,HG=GE=IE=n,
∴AF=AE=OA﹣OE=3﹣m,
∴AG=GE+AE=n+3﹣m,
∵DA=OA=3,
∴DH=DF=DA﹣AF=3﹣(3﹣m)=m,
∴DG=DH+HG=m+n,
∵DG2+AG2=DA2,∴(m+n)2+(n+3﹣m)2=32,
∴化简得:m2﹣3m+n2+3n=0,
配方得:(m﹣![]() )2+(n+
)2+(n+![]() )2=
)2=![]() ,
,
∴点I(m,n)与定点Q(![]() ,﹣
,﹣![]() )的距离为
)的距离为![]() ,
,
∴点I在以点Q(![]() ,﹣
,﹣![]() )为圆心,半径为
)为圆心,半径为![]() 的圆在第一象限的弧上运动,
的圆在第一象限的弧上运动,
∴当点I在线段CQ上时,CI最小,
∵CQ=![]() ,∴CI=CQ﹣IQ=
,∴CI=CQ﹣IQ=![]() ,
,
∴CI最小值为![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
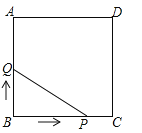
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A.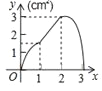 B.
B.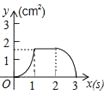 C.
C.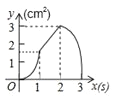 D.
D.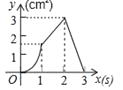
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.

(1)求证:△DAC∽△EBC;
(2)求△ABC与△DEC的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
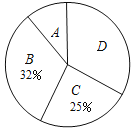
【题目】某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)本次调查的学生共有 人;在扇形统计图中,B所对应的扇形的圆心角的度数是 ;
(2)将条形统计图补充完整;
(3)在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运如红脸代表忠心耿直,黑脸代表强悍勇猛现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.

(1)请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率(图案为“红脸”的两张卡片分别记为![]() 、
、![]() ,图案为“黑脸”的卡片记为
,图案为“黑脸”的卡片记为![]() );
);
(2)若第一次抽出后不放回,请直接写出求抽出的两张卡片上的图案都是“红脸”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
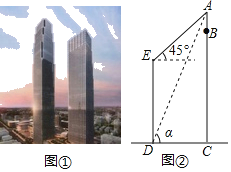
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AB=5cm,BC=7cm,S△ABC=14cm2,点P从点B出发,以3cm∕s的速度沿边BC向终点C运动,过点P作PQ⊥BC交折线BAC于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
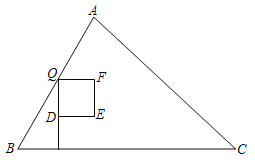
(1)∠C的度数为 ;
(2)当点P不与点C重合,且点F落在边AC上时x的值为 .
(3)当点P不与点B,C重合时,求y关于x的函数解析式;
(4)当直线BD平分△ABC的面积时,直接写出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com