
����Ŀ����֪����������A��O��B��ʾ�����ֱ�Ϊ��3��0��1����PΪ����������һ�㣬���ʾ����Ϊx��
��1�������P����A����B�ľ�����ȣ���ôx= ��
��2����x= ʱ����P����A����B�ľ���֮����6��
��3������P����A����B�ľ���֮����С����x��ȡֵ��Χ�� ��
��4���������ϣ���M��N��ʾ�����ֱ�Ϊx1 �� x2 �� ���ǰ�x1 �� x2֮��ľ���ֵ������M��N֮��ľ��룬��MN=|x1��x2|������P��ÿ��3����λ���ȵ��ٶȴӵ�O��������ĸ������˶�ʱ����E��ÿ��1����λ���ȵ��ٶȴӵ�A��������ĸ������˶�����F��ÿ��4����λ���ȵ��ٶȴӵ�B��������ĸ������˶�����������ͬʱ��������ô�˶� ��ʱ����P����E����F�ľ�����ȣ�
���𰸡�-1����4��2����3��x��1��![]() ��2
��2
���������⣺��1��������ã�|x������3��|=|x��1|��
���x=��1��
��2����AB=|1������3��|=4����P����A����B�ľ���֮����6��
���P�ڵ�A�����ʱ����3��x+1��x=6��
���x=��4��
��P�ڵ�B���ұ�ʱ��x��1+x������3��=6��
���x=2��
����������x=��4��2��
��3��������֮���߶���̿�֪����P��AB֮��ʱ��P����A����B�ľ���֮����С��
����x��ȡֵ��Χ�ǩ�3��x��1��
��4�����˶�ʱ��Ϊt����P��ʾ����Ϊ��3t����E��ʾ����Ϊ��3��t����F��ʾ����Ϊ1��4t��
�ߵ�P����E����F�ľ�����ȣ�
��|��3t������3��t��|=|��3t����1��4t��|��
�ੁ2t+3=t��1��2t+3=1��t��
���t=![]() ��t=2��
��t=2��
�ʴ�Ϊ����1����1����2����4��2����3����3��x��1����4��![]() ��2��
��2��
��1�����������������ľ���ı�ʾ�г�������⼴�ɣ�
��2������AB�ľ���Ϊ4��С��6���ֵ�P�ڵ�A����ߺ͵�B���ұ���������ֱ��г����̣�Ȼ����⼴�ɣ�
��3����������֮���߶���̿�֪��P�ڵ�AB֮��ʱ��P����A����B�ľ���֮����С��̣�Ȼ��д��x��ȡֵ��Χ���ɣ�
��4�����˶�ʱ��Ϊt���ֱ��ʾ����P��E��F����ʾ������Ȼ����������ľ���ı�ʾ�г�����ֵ���̣�Ȼ����⼴�ɣ�


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ɫ�����������ɫ�������εı߳���ȣ���������Ƕͼ�����������£���ɫ�������η��������У�����һ�е��������θ���������һ����һ������������֮��Ŀ�϶�ú�ɫ����������Ƕ��������1��2��3��ͼ������ͼ����ʾ����������ȥ�����n��ͼ���У���ɫ�������κͰ�ɫ�������εĸ����ֱ��������ú�n�Ĵ���ʽ��ʾ��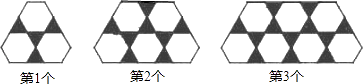
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı��� ![]() �У�
�У� ![]() �ֱ�Ϊ��
�ֱ�Ϊ�� ![]() ���е㣬
���е㣬 ![]() �ǶԽ��ߣ�����
�ǶԽ��ߣ����� ![]() ��
�� ![]() ��
�� ![]() ���ӳ����ڵ�
���ӳ����ڵ� ![]() ��
��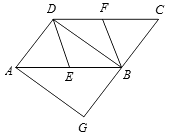
��1����֤�� ![]() ��
��
��2���� ![]() ����֤���ı���
����֤���ı��� ![]() �����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������֧����������籭Ԥѡ���н������ֱ�Ϊ9��9��x��7�����������ݵ�������ƽ����ǡ����ȣ�������е�xֵ�Լ��������ݵı��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC=100�㣬��ACB=40�㣬��ABC��ƽ����BD��AC�ڵ�D����ACB��ƽ����CP��BD�ڵ�D��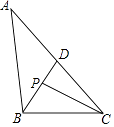
��1��BD��AC��λ�ù�ϵ�� ��
��2�����BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ƿ���x2��x��2019��0������ʵ����������2+����ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԥ���½������Ὣ����Լ69 000 000�˴βιۣ���69 000 000�ÿ�ѧ��������ʾ��ȷ���ǣ� ��
A.0.69��108
B.6.9��106
C.6.9��107
D.69��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��������ABC�У���ACB=90�㣬����ABC�Ƶ�C��ʱ�뷽����ת��ʹ��A����AB���ϵĵ�D�����õ���DEC��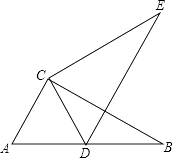
��1����B�Ķ�Ӧ���ǵ� �� BC�Ķ�Ӧ�߶��� ��
��2���жϡ�ACD����״��
��3����AD=CD�����B�͡�BCE�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com