
分析 (1)由可获得利润P=-$\frac{1}{100}$(x-60)2+41(万元),即可知当x=60时,P最大,最大值为41,继而求得5年所获利润的最大值;
(2)首先求得前两年的获利最大值,注意前两年:0≤x≤50,此时因为P随x的增大而增大,所以x=50时,P值最大;然后后三年:设每年获利y,设当地投资额为a,则外地投资额为100-a,即可得函数y=P+Q=[-$\frac{1}{100}$(a-60)2+41]+[-$\frac{99}{100}$a2+$\frac{294}{5}$a+160],整理求解即可求得最大值,则可求得按规划实施,5年所获利润(扣除修路后)的最大值;
(3)比较可知,该方案是具有极大的实施价值.
解答 解:(1)∵P=$-\frac{1}{100}$(x-60)2+41,
∴当x=60时,p取最大值41,
5年所获利润的最大值=41×5=205;
(2)①∵a=$-\frac{1}{100}$<0,
∴当x<60时,p随x增大而增大,
∵拨出50万进行修路,
∴当地政府对该特产的销售投资为50万,
∴当x=50时,p取最大值,代入可得p=40,
则这两年在当地销售的最大利润=40×2=80;
后三年:设每年获利y,设当地投资额为a,则外地投资额为100-a,
∴Q=-$-\frac{99}{100}$[100-(100-a)]2+$\frac{294}{5}$[100-(100-a)]+160=-$\frac{99}{100}$a2+$\frac{294}{5}$a+160,
∴y=P+Q=[-$\frac{1}{100}$(a-60)2+41]+[-$\frac{99}{100}$a2+$\frac{294}{5}$a+160]=-a2+60a+165=-(a-30)2+1065,
∴当a=30时,y最大且为1065,
∴这三年的获利最大为1065×3=3195(万元),
∴5年所获利润(扣除修路后)的最大值是:80+3195-50×2=3175(万元).
(3)有很大的实施价值.
规划后5年总利润为3175万元,不实施规划方案仅为205万元,故具有很大的实施价值.
点评 此题考查了二次函数的实际应用问题.解题的关键是理解题意,找到合适函数取得最大值,是解此题的关键,还要注意后三年的最大值的求解方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
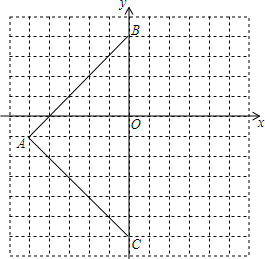 如图,三角形ABC在平面直角坐标系中,三个顶点坐标分别为A(-5,-1)、B(0,4)、C(0,-6).
如图,三角形ABC在平面直角坐标系中,三个顶点坐标分别为A(-5,-1)、B(0,4)、C(0,-6).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
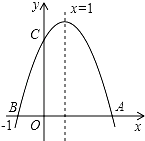 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标是(-1,0),对称轴为直线x=1,下面的四个结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标是(-1,0),对称轴为直线x=1,下面的四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com