
【题目】
如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.
⑴求证:PB是⊙O的切线;
⑵连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
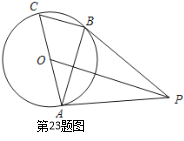
【答案】(1)详见解析;(2)2.
【解析】
试题分析:(1)连接OB,由AC是⊙O的直径可得∠ABC=90°,∠C+∠BAC=90°.再由OA=OB可得∠BAC=∠OBA. 又因∠PBA=∠C,所以∠PBA+∠OBA=90°,即PB⊥OB.即可判定PB是⊙O的切线.(2)可证△ABC∽△PBO,根据相似三角形的性质即可求BC的长.
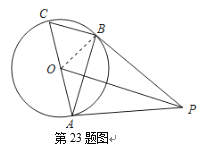
试题解析: ⑴证明:如图所示,连接OB.
∵AC是⊙O的直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵OA=OB,
∴∠BAC=∠OBA.
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,即PB⊥OB.
∴PB是⊙O的切线.
⑵解:⊙O的半径为![]() ,∴OB=
,∴OB=![]() ,AC=
,AC=![]() .
.
∵OP∥BC,
∴∠BOP=∠OBC=∠C.
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴![]() ,即
,即![]() .
.
∴BC=2.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=![]() ,求⊙O的面积.
,求⊙O的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在做“化简(2x+k)(3x+2)﹣6x(x+3)+5x+16并求x=2时的值”一题时,错将x=2看成x=﹣2,但结果却和正确答案一样,由此,你能推算出k值吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )

A. 6 B. ![]() C. 9 D.
C. 9 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (2016四川达州第15题)如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com