
【题目】如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD.AG. 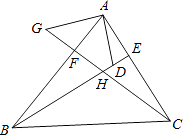
(1)求证:AD=AG;
(2)AD与AG的位置关系如何.
【答案】
(1)解:∵BE、CF分别是AC、AB两边上的高,
∴∠AFC=∠BFC=∠BEC=∠BEA=90°
∴∠BAC+∠ACF=90°,∠BAC+∠ABE=90°,∠G+∠GAF=90°,
∴∠ABE=∠ACF.
在△ABD和△GCA中,
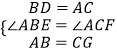 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA,
(2)解:结论:AG⊥AD.
理由:∵△ABD≌△GCA(SAS),
∴∠BAD=∠G,
∴∠BAD+∠GAF=90°,
∴AG⊥AD.

【解析】(1)先由条件可以得出∠ABE=∠ACF,就可以得出△ABD≌△GCA,就有AD=GA,∠BAD=∠G;(2)结论:AG⊥AD.由(1)可以得出∠GAD=90°,进而得出AG⊥AD.


科目:初中数学 来源: 题型:
【题目】今年,我国一些地区遭受旱灾,旱灾牵动全国人民的心.图(1)是我市某中学“献爱心,抗旱灾”自愿捐款活动中学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1450人).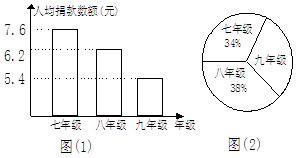
(1)初三学生共捐款多少元?
(2)该校学生平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新田为实现全县“脱贫摘帽”,2018年2月已统筹整合涉农资金235000000元,撬动800000000元金融资本参与全县脱贫攻坚工作,请将235000000用科学记数法表示为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形ABC的三个顶点坐标分别是A(-4,-1),B(-1,4),C(1,1),点A经过平移后对应点为A1(-2,1),将三角形ABC作同样的平移得到三角形A1B1C1,写出B1、C1两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强市民的节水意识,某市对居民用水实行“阶梯收费”.规定每户每月不超过月用水标准量部分的水价为1.5元/吨,超过月用水标准量部分的水价为2.5元/吨.该市小明家5月份用水12吨,交水费20元,该市规定的每户月用水标准量是多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com