
已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于 点E,∠BAC=45°.
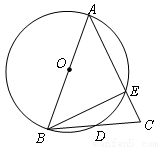
(1)∠EBC求的度数;
(2)求证:BD=CD.
(1)20°;(2)证明见解析.
【解析】
试题分析:(1)根据等腰三角形的性质得∠ABC=∠C,再根据三角形内角和定理得到∠C=70°,然后根据圆周角定理得到∠AEB=90°,再利用互余计算∠EBC;
(2)连结AD,根据圆周角定理得到∠ADB=90°,即AD⊥BC,然后根据等腰三角形的性质即可得到结论.
试题解析:(1)【解析】
∵AB=AC,
∴∠ABC=∠C,
∵∠BAC=40°,
∴∠C= (180°-40°)=70°,
(180°-40°)=70°,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠EBC=90°-∠C=20°;
(2)证明:连结AD,如图,

∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
而AB=AC,
∴BD=DC.
考点:1.圆周角定理;2.等腰三角形的性质.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源:2014-2015学年江苏省实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
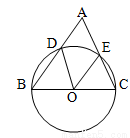
如图,以△ABC的边BC为直径的圆O分别交AB、AC于点D、E,连接OD、OE,若∠ A=65°,则∠ DOE= °.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期第一次单元考试数学试卷(解析版) 题型:解答题
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,①猜想 DE与AB的关系?并加以证明。②若P是AB延长线一点,Q为BC一点,其他条件不变,结论成吗?画图并证明

(友情引导:若不知道,你可以动手去量发现结论。若不会,P是动点,你可以把P运动到特殊的地方,发现现在可利用什么性质?接下来证明。发现缺少什么?就补什么。若还不会,你能发现有线段相等吗?尝试证明,你会有惊喜。)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期第一次单元考试数学试卷(解析版) 题型:选择题
如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD=( )

A. 150° B.300° C. 210° D. 330°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期第一次单元考试数学试卷(解析版) 题型:选择题
用直尺和圆规作一个角的角平分 线,其正确的依据是( )
A.AAS B.SSS C.SAS D.AS A
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴华顾庄等三校九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.以点C为圆心,r为半径画圆,若圆C 与斜边AB有且只有一个公共点时,则r的取值范围是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴华顾庄等三校九年级上学期期中考试数学试卷(解析版) 题型:填空题
抛掷一枚质地均匀的硬币2次,2次抛掷的结果都是正面朝上的概率是_ __.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com