
【题目】Rt△ABC中,∠C=90°,AC=![]() ,点D为BC边上一点,且BD=AD,∠ADC=60°,则△ABC的周长为_____.(结果保留根号)
,点D为BC边上一点,且BD=AD,∠ADC=60°,则△ABC的周长为_____.(结果保留根号)
科目:初中数学 来源: 题型:
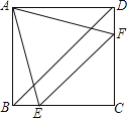
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法不正确的是( )

A.△ABE的面积=△BCE的面积B.∠AFG=∠AGF
C.BH=CHD.∠FAG=2∠ACF
查看答案和解析>>
科目:初中数学 来源: 题型:
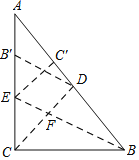
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B′处,展开后,再沿BE折叠,使点C落在BA边上的C′处,CD与BE交于点F.
(1)求AC′的长度;
(2)求CE的长度;
(3)比较四边形EC′DF与△BCF面积的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
(2)若B型号足球数量不少于A型号足球数量的![]() ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com