
(本题满分10分)阅读理【解析】
如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:

(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
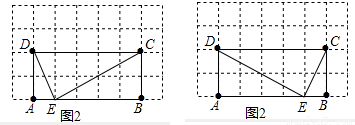
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试确定E点位置.
(1) 点E是四边形ABCD的AB边上的相似点;(2)详见解析;(3)E在BC中点
【解析】
试题分析:(1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
(2)根据两个直角三角形相似得到强相似点的两种情况即可.
(3)因为点E是梯形ABCD的AB边上的一个强相似点,所以就有相似三角形出现,根据相似三角形的对应线段成比例,可以判断出BC和BE的数量关系,从而可求出解.
试题解析::(1)点E是四边形ABCD的边AB上的相似点.
理由:∵∠A=55°,
∴∠ADE+∠DEA=125°.
∵∠DEC=55°,
∴∠BEC+∠DEA=125°.
∴∠ADE=∠BEC.(2分)
∵∠A=∠B,
∴△ADE∽△BEC.
∴点E是四边形ABCD的AB边上的相似点.
(2)作图如下:
(3)∵点E是四边形ABCM的边AB上的一个强相似点,
∴△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM.
由折叠可知:△ECM≌△DCM,
∴∠ECM=∠DCM,CE=CD,
∴∠BCE=1/3 ∠BCD=30°,BE=1/2 CE=1/2 AB,即点E为AB中点。
考点: 相似形综合题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:填空题
河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 .
(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市滨湖区九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,已知AB是⊙O直径,∠AOC=130°,则∠D等于( )

A.65° B.25° C.15 D.35°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期高效课堂调研数学试卷(解析版) 题型:解答题
(本题满分7分)如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:
(1)第④个图形中阴影部分小正方形的个数为 ;

(2)是否存在阴影部分小正方形的个数是整个图形中小正方形个数的 ?如果存在,是第几个图形;如果不存在,请说明理由.
?如果存在,是第几个图形;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期高效课堂调研数学试卷(解析版) 题型:填空题
如图,已知梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= ,S△COB:S△COD= .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题7分)如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).

(1)画出拼成的矩形的简图(请在简图上标明x与y);
(2)求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市新区八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,直线 是一条河,A、B两地相距10
是一条河,A、B两地相距10 ,A、B两地到
,A、B两地到 的距离分别为8
的距离分别为8 、14
、14 ,
,
欲在 上的某点M处修建一个水泵站,向A、B两地供水,现有如下四种铺设方案,图中实线表示铺设的
上的某点M处修建一个水泵站,向A、B两地供水,现有如下四种铺设方案,图中实线表示铺设的
管道,则铺设的管道最短的是( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com