
【题目】如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是![]() 上任意一点,过C作⊙O的切线分别交PA,PB于D,E.(1)若△PDE的周长为10,则PA的长为___ __,(2)连结CA、CB,若∠P=50°,则∠BCA的度数为___ __度.
上任意一点,过C作⊙O的切线分别交PA,PB于D,E.(1)若△PDE的周长为10,则PA的长为___ __,(2)连结CA、CB,若∠P=50°,则∠BCA的度数为___ __度.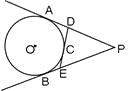
【答案】5,115
【解析】
(1)由于PA、PB、DE都是⊙O的切线,可根据切线长定理将△PDE的周长转化为切线PA、PB的长.
(2)根据切线长定理即可证得△PEF 周长等于2PA即可求解;根据切线的性质以及四边形的内角和定理即可求得∠AOB的度数,然后根据∠EOF=![]() ∠AOB即可求出∠BCA的度数.
∠AOB即可求出∠BCA的度数.
解:(1)∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=10;
∴PA=PB=5;
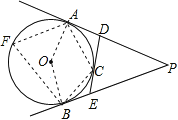
(2)连接OA、OB、AC、BC,在⊙O上取一点F,连接AF、BF,
∵PA、PB分别切⊙O 于A、B;
∴∠PAO=∠PRO=90°
∴∠AOB=360°-90°-90°-50°=130°;
∴∠AFB=![]() ∠AOB=65°,
∠AOB=65°,
∵∠AFB+∠BCA=180°
∴∠BCA=180°-65°=115°;
故答案是:5,115°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.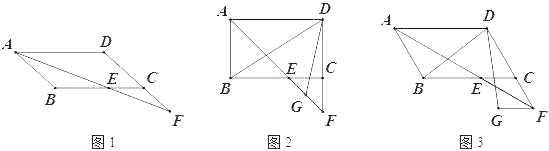
查看答案和解析>>
科目:初中数学 来源: 题型:
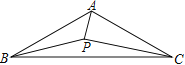
【题目】如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为( )
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数的图象经过点A(2,3)与点B(0,5)。
(1)求此一次函数的解析式。
(2)若P点为此一次函数图象上一点,且△POB的面积为10.求点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
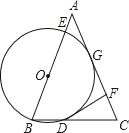
【题目】如图,AB=AC,点O在AB上,⊙O过点B,分别与BC、AB交于D、E,过D作DF⊥AC于F.
(1)求证:DF是⊙O的切线;
(2)若AC与⊙O相切于点G,⊙O的半径为3,CF=1,求AC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠BAC=90°,AB=AC,在△ABC外作∠ACM=![]() ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
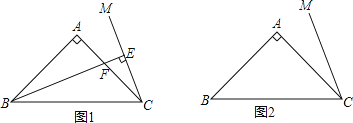
(1)当点D在线段BC上时,如图1所示,①∠EDC= °;
②探究线段DF与EC的数量关系,并证明;
(2)当点D运动到CB延长线上时,请你画出图形,并证明此时DF与EC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:

根据所给信息,解决下列问题:
(1)a= ,b= ;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
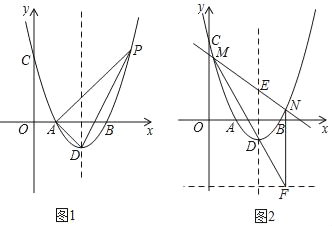
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com