
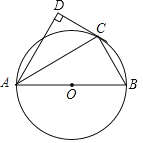
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
【答案】(1)见解析;(2)π
【解析】
(1)连接OC,只需证明∠OCD=90°即可;
(2)由圆周角定理得出∠ACB=90°,即可求得∠OCB=60°,得到△OBC是等边三角形,可求得半径为3,弧BC的圆心角度数,再利用弧长公式求得结果即可.
解:(1)证明:连接OC,
∵AC是∠BAD的平分线,
∴∠CAD=∠BAC,
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
∴∠OCD=∠D=90°,
∴CD是⊙O的切线;
(2)解:∵∠ACD=60°,
∴∠OCA=30°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠OCB=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴OB=OC=BC=3,∠COB=60°,
∴![]() 的长:
的长:![]() .
.


科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 | m | 40% |
合格 | 6 | n% |
待合格 | 3 | 6% |

请根据以上信息,解答下列问题:
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 图象的顶点在一次函数
图象的顶点在一次函数![]() 的图象上,则称
的图象上,则称![]() 为
为![]() 的伴随函数,如:
的伴随函数,如:![]() 是
是![]() 的伴随函数.
的伴随函数.
(1)若![]() 是
是![]() 的伴随函数,求直线
的伴随函数,求直线![]() 与两坐标轴围成的三角形的面积;
与两坐标轴围成的三角形的面积;
(2)若函数![]() 的伴随函数
的伴随函数![]() 与
与![]() 轴两个交点间的距离为4,求
轴两个交点间的距离为4,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
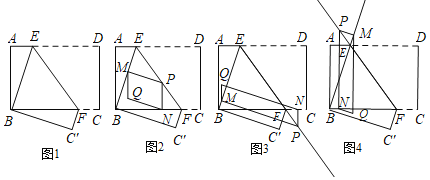
【题目】操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:若DE=a,CF=b.
①如图3,当点P在线段EF的延长线上运动时,试用含a、b的式子表示QM与QN之间的数量关系,并证明;
②如图4,当点P在线段FE的延长线上运动时,请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
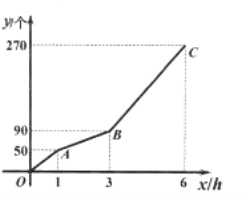
【题目】甲、乙两台机器共同加工一批零件,一共用了![]() 小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数
小时.在加工过程中乙机器因故障停止工作,排除故障后,乙机器提高了工作效率且保持不变,继续加工.甲机器在加工过程中工作效率保持不变.甲、乙两台机器加工零件的总数![]() (个)与甲加工时间
(个)与甲加工时间![]() 之间的函数图象为折线
之间的函数图象为折线![]() ,如图所示.
,如图所示.
(1)这批零件一共有 个,甲机器每小时加工 个零件,乙机器排除故障后每小时加工 个零件;
(2)当![]() 时,求
时,求![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
(3)在整个加工过程中,甲加工多长时间时,甲与乙加工的零件个数相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有学生3000人,现欲开展学校社团活动,准备组建摄影社、国学社、篮球社、科技制作社四个社团.每名学生最多只能报一个社团,也可以不报.为了估计各社团人数,现在学校随机抽取了50名学生做问卷调查,得到了如图所示的两个不完全统计图.
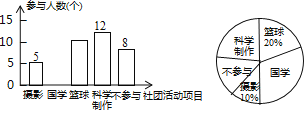
结合以上信息,回答下列问题:
(1)本次抽样调查的样本容量是_____;
(2)请你补全条形统计图,并在图上标明具体数据;
(3)求参与科技制作社团所在扇形的圆心角度数;
(4)请你估计全校有多少学生报名参加篮球社团活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
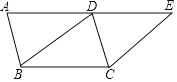
【题目】如图,四边形ABCD是平行四边形,延长AD至点E,使DE=AD,连接BD.
(1)求证:四边形BCED是平行四边形;
(2)若DA=DB=2,cosA=![]() ,求点B到点E的距离.
,求点B到点E的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
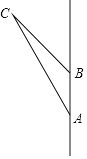
【题目】如图,汽车在一条南北走向的公路上以每小时60千米的速度匀速向北行驶.当汽车在A处时,某信号塔C在它的北偏西30°方向,汽车前行2分钟.到达B处,此时信号塔C在它的北偏西45°方向.
(1)求AB的距离.
(2)求信号塔C到该公路的距离.(![]() ,结果精确到0.1千米)
,结果精确到0.1千米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com