
【题目】若二次函数![]() 图象的顶点在一次函数
图象的顶点在一次函数![]() 的图象上,则称
的图象上,则称![]() 为
为![]() 的伴随函数,如:
的伴随函数,如:![]() 是
是![]() 的伴随函数.
的伴随函数.
(1)若![]() 是
是![]() 的伴随函数,求直线
的伴随函数,求直线![]() 与两坐标轴围成的三角形的面积;
与两坐标轴围成的三角形的面积;
(2)若函数![]() 的伴随函数
的伴随函数![]() 与
与![]() 轴两个交点间的距离为4,求
轴两个交点间的距离为4,求![]() ,
,![]() 的值.
的值.
【答案】(1)8;(2)![]() ,
,![]() .
.
【解析】
(1)先求出二次函数的顶点,再把顶点代入一次函数求出p,再求出一次函数与坐标轴的交点坐标,再利用三角形的面积公式求解;
(2)先根据函数![]() 与
与![]() 轴两个交点间的距离为4,求出n,再求出二次函数的顶点,将顶点代入一次函数即可求解.
轴两个交点间的距离为4,求出n,再求出二次函数的顶点,将顶点代入一次函数即可求解.
解:(1)![]() ,
,
![]() 其顶点坐标为
其顶点坐标为![]() ,
,
![]() 是
是![]() 的伴随函数,
的伴随函数,
![]() 在一次函数
在一次函数![]() 的图象上,
的图象上,
![]() .
.
![]() ,
,
![]() 一次函数为:
一次函数为:![]() ,
,
![]() 一次函数与坐标轴的交点分别为
一次函数与坐标轴的交点分别为![]() ,
,![]() ,
,
![]() 直线
直线![]() 与两坐标轴围成的三角形的两直角边长度都为
与两坐标轴围成的三角形的两直角边长度都为![]() ,
,
![]() 直线
直线![]() 与两坐标轴围成的三角形的面积为:
与两坐标轴围成的三角形的面积为:![]() .
.
(2)设函数![]() 与
与![]() 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
∵函数![]() 与
与![]() 轴两个交点间的距离为4,
轴两个交点间的距离为4,
![]() ,
,
解得,![]() ,
,
![]() 函数
函数![]() 为:
为:![]() ,
,
![]() 其顶点坐标为
其顶点坐标为![]() ,
,
![]() 是
是![]() 的伴随函数,
的伴随函数,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
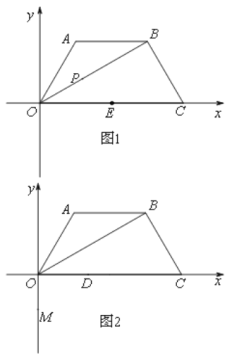
【题目】如图1,等腰梯形OABC的底边OC在x轴上,AB∥OC,O为坐标原点,OA = AB =BC,∠AOC=60°,连接OB,点P为线段OB上一个动点,点E为边OC中点.
(1)连接PA.PE,求证:PA=PE;
(2)连接PC,若PC+PE=2![]() ,试求AB的最大值;
,试求AB的最大值;
(3)在(2)在条件下,当AB取最大值时,如图2,点M坐标为(0,-1),点D为线段OC上一个动点,当D点从O点向C点移动时,直线MD与梯形另一边交点为N,设D点横坐标为m,当△MNC为钝角三角形时,求m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
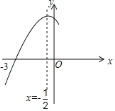
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:①
,结合图象分析下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④一元二次方程
的增大而增大;④一元二次方程![]() 的两根分别为
的两根分别为![]() ,
,![]() ;⑤
;⑤![]() ;⑥若
;⑥若![]() ,
,![]() 为方程
为方程![]() 的两个根,则
的两个根,则![]() 且
且![]() ,其中正确的结论有( )
,其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:
经济学家将家庭或个人在食品消费上的支出与总消费支出的比值称作恩格尔系数.即:恩格尔系数=![]() ×100%.恩格尔系数可以用来刻划不同的消费结构,也能间接反映一个国家(地区)不同的发展阶段.联合国粮农组织的规定如表所示:
×100%.恩格尔系数可以用来刻划不同的消费结构,也能间接反映一个国家(地区)不同的发展阶段.联合国粮农组织的规定如表所示:
恩格尔系数 大于或等于60% | 恩格尔系数 在50%~60%之间 | 恩格尔系数 在40%~50%之间 | 恩格尔系数 在30%~40%之间 | 恩格尔系数 小于30% |
绝对贫困 | 温 饱 | 小 康 | 富 裕 | 最富裕 |
(注:在50%﹣60%之间是指含50%,不含60% 的所有数据,以此类推)
材料2:
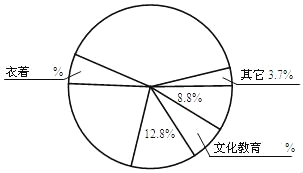
2014年2月22日国家统计局上海调查总队报道:2013年上海市居民家庭生活消费总支出人均13425元.其中食品支出人均5334元(包括粮食支出450元,蔬菜及制品支出438元,肉禽蛋奶及制品支出1393元,水产品支出581元),衣着支出人均771元,居住支出人均2260元,公用事业支出人均694元,交通通信支出人均1719元,文化教育支出人均964元,医疗保健支出人均1181元,其它支出人均502元.
根据上述材料,
(1)分别计算出“食品”、“衣着”、“居住”、“公用事业”、“交通通信”、“文化教育”和“医疗保健”占家庭生活消费总支出的百分比,并补充完成下列扇形统计图.(百分号前保留一位小数,圆心角精确到1°)
(2)计算上海市居民的恩格尔系数,并判断2013年上海市居民的生活水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是___________.(写出所有正确结论的序号)
①AM平分∠CAB;
②AM2=ACAB;
③若AB=4,∠APE=30°,则![]() 的长为
的长为![]() ;
;
④若AC=3,BD=1,则有CM=DM=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
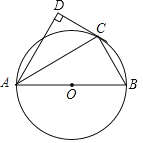
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
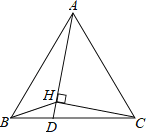
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组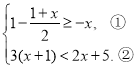
请结合题意填空,完成本题的解答。
(Ⅰ)解不等式①,得_____________;
(Ⅱ)解不等式②,得_____________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com