
【题目】材料1:
经济学家将家庭或个人在食品消费上的支出与总消费支出的比值称作恩格尔系数.即:恩格尔系数=![]() ×100%.恩格尔系数可以用来刻划不同的消费结构,也能间接反映一个国家(地区)不同的发展阶段.联合国粮农组织的规定如表所示:
×100%.恩格尔系数可以用来刻划不同的消费结构,也能间接反映一个国家(地区)不同的发展阶段.联合国粮农组织的规定如表所示:
恩格尔系数 大于或等于60% | 恩格尔系数 在50%~60%之间 | 恩格尔系数 在40%~50%之间 | 恩格尔系数 在30%~40%之间 | 恩格尔系数 小于30% |
绝对贫困 | 温 饱 | 小 康 | 富 裕 | 最富裕 |
(注:在50%﹣60%之间是指含50%,不含60% 的所有数据,以此类推)
材料2:
2014年2月22日国家统计局上海调查总队报道:2013年上海市居民家庭生活消费总支出人均13425元.其中食品支出人均5334元(包括粮食支出450元,蔬菜及制品支出438元,肉禽蛋奶及制品支出1393元,水产品支出581元),衣着支出人均771元,居住支出人均2260元,公用事业支出人均694元,交通通信支出人均1719元,文化教育支出人均964元,医疗保健支出人均1181元,其它支出人均502元.
根据上述材料,
(1)分别计算出“食品”、“衣着”、“居住”、“公用事业”、“交通通信”、“文化教育”和“医疗保健”占家庭生活消费总支出的百分比,并补充完成下列扇形统计图.(百分号前保留一位小数,圆心角精确到1°)
(2)计算上海市居民的恩格尔系数,并判断2013年上海市居民的生活水平.
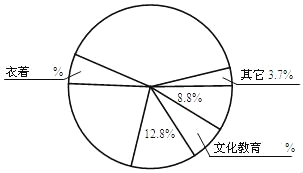
【答案】(1)食品”、“衣着”、“居住”、“公用事业”、“交通通信”、“文化教育”和“医疗保健”占家庭生活消费总支出的百分比分别为:39.7%,5.7%,16.8%,5.3%,12.8%,7.2%,8.8%;补图见解析;(2)恩格尔系数是39.7%,是富裕生活.
【解析】
(1)分别计算出“食品”、“衣着”、“居住”、“公用事业”、“交通通信”、“文化教育”和“医疗保健”占家庭生活消费总支出的百分比,再补充完成扇形统计图即可求解;
(2)根据上海市居民的恩格尔系数即可作出判断.
解:(1)“食品”、“衣着”、“居住”、“公用事业”、“交通通信”、“文化教育”和“医疗保健”占家庭生活消费总支出的百分比分别为:
5334÷13425×100%=39.7%,
771÷13425×100%=5.7%,
2260÷13425×100%=16.8%,
694÷13425×100%=5.3%,
1719÷13425×100%=12.8%
964÷13425×100%=7.2%,
1181÷13425×100%=8.8%,
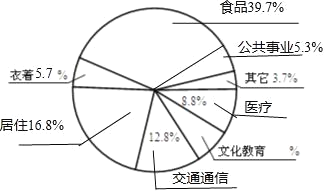
扇形统计图如图:
(2) 恩格尔系数=![]() ×100%=39.7%,
×100%=39.7%,
上海市居民的恩格尔系数是39.7%,是富裕生活.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 | m | 40% |
合格 | 6 | n% |
待合格 | 3 | 6% |

请根据以上信息,解答下列问题:
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地间的直线公路长为![]() 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发
千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发![]() 小时,途中轿车出现了故障,停下维修,货车仍继续行驶.
小时,途中轿车出现了故障,停下维修,货车仍继续行驶.![]() 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离
小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离![]() (千米)与轿车所用的时间
(千米)与轿车所用的时间![]() (小时)的关系如图所示,请结合图象解答下列问题:
(小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是_______千米/小时;轿车的速度是_______千米/小时;![]() 值为_______.
值为_______.
(2)求轿车距其出发地的距离![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数关系式并写出自变量
(小时)之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)请直接写出货车出发多长时间两车相距![]() 千米.
千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 图象的顶点在一次函数
图象的顶点在一次函数![]() 的图象上,则称
的图象上,则称![]() 为
为![]() 的伴随函数,如:
的伴随函数,如:![]() 是
是![]() 的伴随函数.
的伴随函数.
(1)若![]() 是
是![]() 的伴随函数,求直线
的伴随函数,求直线![]() 与两坐标轴围成的三角形的面积;
与两坐标轴围成的三角形的面积;
(2)若函数![]() 的伴随函数
的伴随函数![]() 与
与![]() 轴两个交点间的距离为4,求
轴两个交点间的距离为4,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
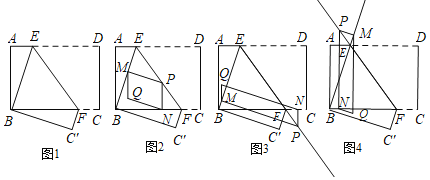
【题目】操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:若DE=a,CF=b.
①如图3,当点P在线段EF的延长线上运动时,试用含a、b的式子表示QM与QN之间的数量关系,并证明;
②如图4,当点P在线段FE的延长线上运动时,请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有学生3000人,现欲开展学校社团活动,准备组建摄影社、国学社、篮球社、科技制作社四个社团.每名学生最多只能报一个社团,也可以不报.为了估计各社团人数,现在学校随机抽取了50名学生做问卷调查,得到了如图所示的两个不完全统计图.
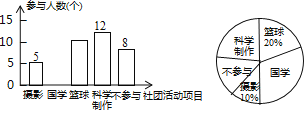
结合以上信息,回答下列问题:
(1)本次抽样调查的样本容量是_____;
(2)请你补全条形统计图,并在图上标明具体数据;
(3)求参与科技制作社团所在扇形的圆心角度数;
(4)请你估计全校有多少学生报名参加篮球社团活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某足球队为了解运动员的年龄情况,作了一次年龄调查,根据足球运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
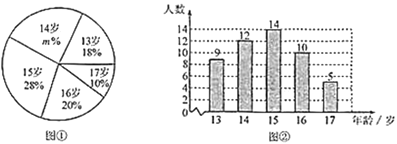
(Ⅰ)本次接受调查的足球运动员人数为______,图①中![]() 的值为______;
的值为______;
(Ⅱ)求统计的这组足球运动员年龄数据的平均数、众数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com