
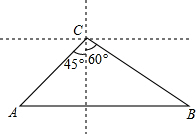
 如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)
如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号) 分析 过C作CP⊥AB于P,在直角三角形ACP中,利用锐角三角函数定义求出AP与PC的长,在直角三角形BCP中,利用锐角三角函数定义求出PB的长,由AP+PB求出AB的长即可.
解答 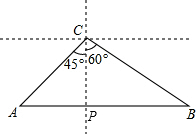 解:过C作CP⊥AB于P,
解:过C作CP⊥AB于P,
∵在Rt△ACP中,AC=40千米,∠ACP=45°,sin∠ACP=$\frac{AP}{AC}$,cos∠ACP=$\frac{CP}{AC}$,
∴AP=AC•sin45°=40×$\frac{\sqrt{2}}{2}$=20$\sqrt{2}$(千米),
CP=AC•cos45°=40×$\frac{\sqrt{2}}{2}$=20$\sqrt{2}$(千米),
∵在Rt△BCP中,∠BCP=60°,tan∠BCP=$\frac{BP}{CP}$,
∴BP=CP•tan60°=20$\sqrt{6}$(千米),
则AB=AP+PB=(20$\sqrt{2}$+20$\sqrt{6}$)千米.
点评 此题考查了解直角三角形的应用-方向角问题,熟练掌握锐角三角函数定义是解本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
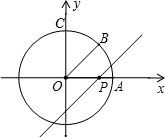 如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.
如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为4$\sqrt{7}$.
如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为4$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:
某天,小华到学校时发现有物品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时,他爸爸从家里出发骑自行车以他3倍的速度给他送遗忘的物品,两人在途中相遇,相遇后小华立即坐爸爸的自行车赶回学校.爸爸和小华在这个过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系如图所示(假设骑自行车和步行的速度始终保持不变).下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com