

分析 (1)根据等腰三角形的性质得到∠FAE=∠FEA,∠AED=∠ADE,由外角的性质得到∠FAE=∠ADE=∠AED,由于∠F=∠FAD,于是得到∠ADE=∠F+∠FAD=2∠F,根据三角形的内角和列方程即可得到结论;
(2)①根据等腰三角形的性质得到∠FAE=∠FEA,∠AED=∠ADE,由外角的性质得到∠FAE=∠ADE=∠AED,由于∠F=∠FAD,于是得到∠ADE=∠F+∠FAD=2∠F,根据三形的内角和列方程求得∠F=36°,由AD⊥BC,根据垂直的定义得到∠ADB=∠ADC=90°,于是得到∠HGD=18°,根据外角的性质得到∠ABC=36°+18°=54°,求出∠ACB=180°-∠BAC-∠ABC=54°,即可得到结论;②由AF=EF,根据线段的和差得到AB+BF=HF+EH,由于AB=AC=AE+CE,等量代换得到AE+CE+BF=HF+EH,由于FH=AE,即可得到结论.
解答 解:(1)∵AF=FE,
∴∠FAE=∠FEA,
∵AD=AE,
∴∠AED=∠ADE,
∴∠FAE=∠ADE=∠AED,
∵AD=DF,
∴∠F=∠FAD,
∵∠ADE=∠F+∠FAD=2∠F,
∴∠FAE=∠AED=2∠F,
∵∠F+∠FAE+∠AEF=180°,
∴∠F=36°;
(2)①∵AF=FE,
∴∠FAE=∠FEA,
∵AH=AE,
∴∠AEH=∠AHE,
∴∠FAE=∠AHE=∠AEH,
∵AH=HF,
∴∠F=∠FAH,
∵∠AHE=∠F+∠FAH=2∠F,
∴∠FAE=∠AEH=2∠F,
∵∠F+∠FAE+∠AEF=180°,
∴∠F=36°,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠AHE=∠AEH=72°,
∴∠DHG=72°,
∴∠HGD=18°,
∴∠ABC=36°+18°=54°,
∵∠ACB=180°-∠BAC-∠ABC=54°,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形;
②CE+BF=EH.
∵AF=EF,
∴AB+BF=HF+EH,
∵AB=AC=AE+CE,
∴AE+CE+BF=HF+EH,
∵FH=AE,
∴CE+BF=EH.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质和判定,三角形的内角和,根据三角形是内角和等于180°列方程求得∠F的度数是解题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向上 | B. | 抛物线的对称轴是x=1 | ||
| C. | 当x=1时,y的最大值为-4 | D. | c=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
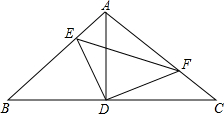 如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )
如图,Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,点E、F分别在边AB和边AC上,且∠EDF=90°,则下列结论不一定成立的是( )| A. | △ADF≌△BDE | B. | S四边形AEDF=$\frac{1}{2}$S△ABC | ||
| C. | BE+CF=$\sqrt{2}$AD | D. | EF=AD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,6) | B. | (5,7) | C. | (4,3) | D. | (-6,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y2>y3>y1 | D. | y3>y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 锐角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com