
【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
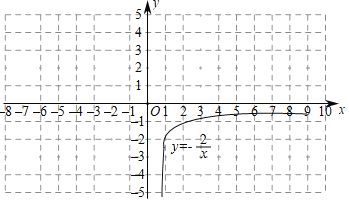
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2
﹣2![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.
【答案】(1)y=|![]() |-3;(2)1,-1;(3)当x>2时,y随x增大而增大;或当x<2时,y随x减小而减小;(4)2
|-3;(2)1,-1;(3)当x>2时,y随x增大而增大;或当x<2时,y随x减小而减小;(4)2![]() ﹣2≤x≤
﹣2≤x≤![]() +4
+4
【解析】
(1)由题意利用待定系数法构建方程组即可解决问题.
(2)由题意利用描点法即可解决问题.
(3)由题意观察图象,写出函数的性质即可.
(4)由题意求出点E,F的坐标即可解决问题.
解:(1)把x=0,y=﹣2;x=2,y=﹣3代入y=|kx﹣1|+b中,得
﹣2=|﹣1|+b,﹣3=|2k﹣1|﹣3
∴b=﹣3,∴k=![]() ,
,
∴y=|![]() |-3.
|-3.
(2)∵x=﹣6时,y=1,
x=6时,y=﹣1,
故答案为1,﹣1.
函数图象如图所示:
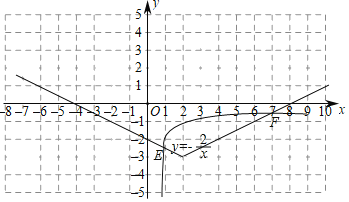
(3)当x>2时,y随x增大而增大;或当x<2时,y随x减小而减小.
(4)由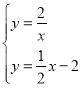 解得
解得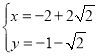 或
或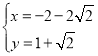 ,
,
∴E(﹣2+2![]() ,﹣1﹣
,﹣1﹣![]() ),
),
同法可得F(2![]() +4,﹣2+
+4,﹣2+![]() )
)
观察图象可知不等式|kx﹣1|+b≤![]() 的解集为:2
的解集为:2![]() ﹣2≤x≤
﹣2≤x≤![]() +4.
+4.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
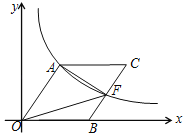
【题目】如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,点A的横纵坐标之比为3:4,反比例函数y=![]() (k>0)在第一象限内的图象经过点A,且与BC交于点F.
(k>0)在第一象限内的图象经过点A,且与BC交于点F.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求OA的长和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)∠A=∠GEF;(2)△BDF≌FEC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别标有数字![]() 、
、![]() 、
、![]() 的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为
的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为![]() (不放回),再从中任意抽取一张,将上面的数字记为
(不放回),再从中任意抽取一张,将上面的数字记为![]() ,这样的数字
,这样的数字![]() ,
,![]() 能使关于
能使关于![]() 的一元二次方程
的一元二次方程![]() 有两个正根的概率为________.
有两个正根的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=﹣x2+2x+3的图象交x轴于点A、B(点A在点B的左侧).若把点B向上平移m(m>0)个单位长度得点B1,若点B1向左平移n(n>0)个单位长度,将与该二次函数图象上的点B2重合;若点B1向左平移(n+2)个单位长度,将与该二次函数图象上的点B3重合.则n的值为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:如图,AD为⊙O的直径。
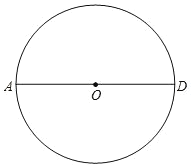
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某化工材料经销商购进一种化工材料若干千克,成本为每千克30元,物价部门规定其销售单价不低于成本价且不高于成本价的2倍,经试销发现,日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图所示.
(元)符合一次函数关系,如图所示.
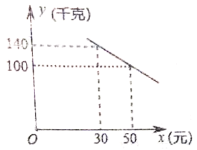
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若在销售过程中每天还要支付其他费用500元,当销售单价为多少时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
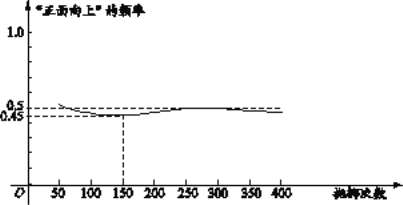
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐至县城有两座远近闻名的南北古塔,清朝道光11年至13年(公元1831--1833年)修建,南塔名为“文运塔”,高30米;北塔名为“凌云塔”.为了测量北塔的高度AB,身高为1.65米的小明在C处用测角仪CD,(如图所示)测得塔顶A的仰角为45°,此时小明在太阳光线下的影长为1.1米,测角仪的影长为1米.随后,他再向北塔方向前进14米到达H处,又测得北塔的顶端A的仰角为60°,求北塔AB的高度.(参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com