
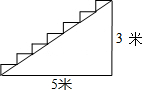
 如图一楼梯宽2m,现要在表面铺地毯,而地毯每平米需要30元,那么购买地毯至少需要480元.
如图一楼梯宽2m,现要在表面铺地毯,而地毯每平米需要30元,那么购买地毯至少需要480元.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
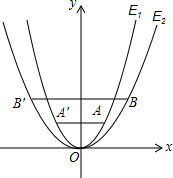 如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
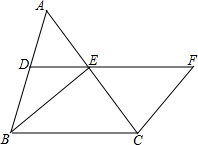 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使EF=BE,连接CF.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使EF=BE,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,2)和(2,3)表示一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(3,-1)到x轴的距离为3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
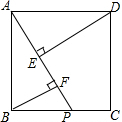 如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.
如图,正方形ABCD中,点P在BC边上,DE⊥AP于点E,BF⊥AP于点F,若BF=x,DE=y,EF=2,求y与x的函数关系式,并画出函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com