
分析 (1)把点A的坐标代入函数解析式来求k的值;
(2)把点B的坐标代入函数解析式进行验证.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$的图象经过点A(2,-3),
∴-3=$\frac{k}{2}$,
解得 k=-6.
则该函数解析式为:y=-$\frac{6}{x}$;
(2)点B(-5,1)是不在这个反比例函数的图象上,理由如下:
由(1)知,函数解析式为:y=-$\frac{6}{x}$.
∵当x=-5时,y=-$\frac{6}{-5}$=$\frac{6}{5}$≠1,
∴点B(-5,1)是不在这个反比例函数的图象上.
点评 本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特征.经过函数的某点一定在函数的图象上.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1+$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | 1-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
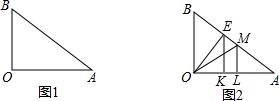 如图1,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,
如图1,已知Rt△AOB中,∠AOB=90°,AO=5,BO=3,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com