
如图1,平面直角坐标系中,直线y=﹣ x+3与抛物线y=ax2+
x+3与抛物线y=ax2+ x+c相交于A,B两点,其中点A在x轴上,点B在y轴上.
x+c相交于A,B两点,其中点A在x轴上,点B在y轴上.
(1)求抛物线的解析式;
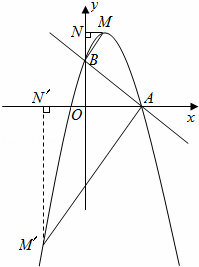
(2)在抛物线上存在一点M,使△MAB是以AB为直角边的直角三角形,求点M的坐标;
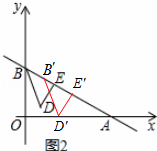
(3)如图2,点E为线段AB上一点,BE=2,以BE为腰作等腰Rt△BDE,使它与△AOB在直线AB的同侧,∠BED=90°,△BDE沿着BA方向以每秒一个单位的速度运动,当点B与A重合时停止运动,设运动时间为t秒,△BDE与△AOB重叠部分的面积为S,直接写出S关于t的函数关系式,并写出自变量t的取值范围.
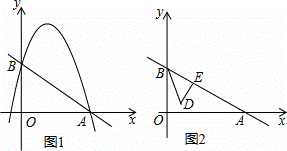
解:(1)对于直线y=﹣ x+3,
x+3,
当y=0时,0=﹣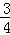 x+3,即x=4,
x+3,即x=4,
∴A(4,0),
当x=0时,y=3,即B(0,3),
把A与B坐标代入y=ax2+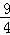 x+c中,得:
x+c中,得: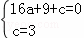 ,
,
解得: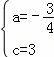 ,
,
则抛物线解析式为y=﹣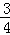 x2+
x2+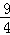 x+3;″
x+3;″
(2)设M坐标为(x,﹣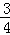 x2+
x2+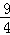 x+3),
x+3),
①当∠MBA=90°时,如图1,作MN⊥y轴,则有∠MNO=90°,
∴∠NMB+∠MBN=90°,
∵∠MBN+∠ABM+∠ABO=180°,
∴∠MBN+∠ABO=90°,
∴∠NMB=∠ABO,
∵∠MNO=∠BOA,
∴△MNB∽△BOA,
∴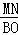 =
=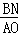 ,
,
即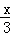 =
= ,
,
解得:x=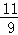 或x=0(舍去),
或x=0(舍去),
当x=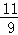 时,y=
时,y=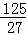 ,即M(
,即M(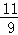 ,
,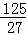 );
);
②当∠BAM′=90°时,易知△AM′N′∽△BAO,∴ ,
,
即 ,解得x=﹣
,解得x=﹣ 或4(舍去),当x=﹣
或4(舍去),当x=﹣ 时,y=﹣
时,y=﹣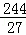 ,
,
即M′(﹣ ,﹣
,﹣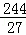 ),
),
则满足条件M的坐标为(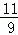 ,
,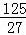 )或(﹣
)或(﹣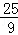 ,﹣
,﹣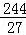 );
);
(3)如图2所示,当D点运动到x轴上时,易知△AD′E′∽△ABO,
∴ ,∴AE′=
,∴AE′=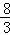 ,∴EE′=AB﹣BE﹣AE′=5﹣2﹣
,∴EE′=AB﹣BE﹣AE′=5﹣2﹣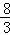 =
=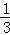 ,
,
∴当0≤t≤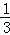 时,S=2;
时,S=2;
当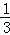 ≤t≤3时,S=﹣
≤t≤3时,S=﹣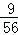 t2+
t2+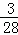 t+
t+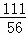 ;
;
当3≤t≤5时,S=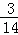 t2﹣
t2﹣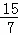 t+
t+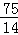 .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
为了开展阳光体育活动,某班计划购买毽子和跳绳两种体育用品,共花费35元,毽子单价3元,跳绳单价5元,购买方案有( )
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000 米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方.求拦截点D 处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和二台B型换气扇共需300元.
(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共40台并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图4,等腰梯形ABCD中,AD∥BC,AE∥DC,∠B=60º,BC=3,△ABE的周长为6,则等腰梯形的周长是( )
(A)8 (B)10 (C)12 (D)16
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1所示,晚上小亮在路灯下散步,在小亮由A处走向B处的过程中,他在地上的影子( )
(A)逐渐变短 (B)逐渐变长
(C)先变短后再变长 (D)先变长后再变短
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com