
分析 先把解析式变形为y=$\frac{{a}^{2}-1}{a}$x+$\frac{1}{a}$,然后分类讨论:当0<a<1或a>1时,根据一次函数的性质确定函数的最小值;当a=1时,函数为常函数,函数值为1.
解答 解:y=$\frac{{a}^{2}-1}{a}$x+$\frac{1}{a}$,
当0<a<1时,函数为一次函数,x=1时,y的值最小,最小值为a;
当a=1,y=1;
当a>1时,函数为一次函数,x=0时,y的值最小,最小值为$\frac{1}{a}$,
故答案为$\left\{\begin{array}{l}{a(0<a<1)}\\{1(a=1)}\\{\frac{1}{a}(a>1)}\end{array}\right.$.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.


科目:初中数学 来源: 题型:解答题
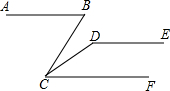 如图,AB∥DE,∠ABC=70°,∠CDE=130°,∠BCF=70°.
如图,AB∥DE,∠ABC=70°,∠CDE=130°,∠BCF=70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,水库大坝的横断面是梯形ABCD,其中AB∥CD,大坝长100米,坝高20米,坡角α=45°,汛期来临前对其进行了加固,改造后的背水面坡度为1:$\sqrt{3}$,坝顶面加宽1米.
如图,水库大坝的横断面是梯形ABCD,其中AB∥CD,大坝长100米,坝高20米,坡角α=45°,汛期来临前对其进行了加固,改造后的背水面坡度为1:$\sqrt{3}$,坝顶面加宽1米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,4,5 | B. | 6,8,10 | C. | $\sqrt{3}$,2,$\sqrt{5}$ | D. | 5,12,13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com