
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
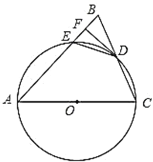
(1)求证:直线![]() 与
与![]() 相切;
相切;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
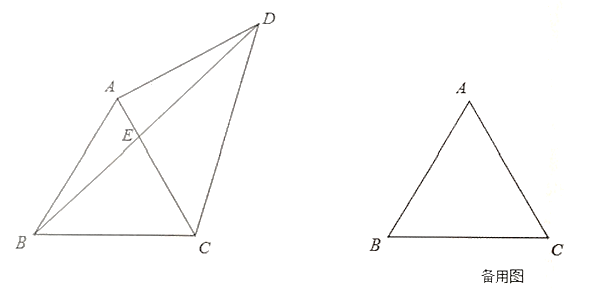
【题目】如图,![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 与点
与点![]() 分别位于直线
分别位于直线![]() 的两侧,且
的两侧,且![]() ,连接
,连接![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,
①当![]() 时,设
时,设![]() (其中
(其中![]() 表示
表示![]() 的面积,
的面积,![]() 表示
表示![]() 的面积),求
的面积),求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
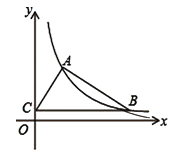
【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=![]()
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
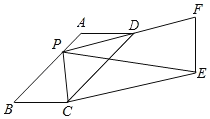
【题目】如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值____.
查看答案和解析>>
科目:初中数学 来源: 题型:
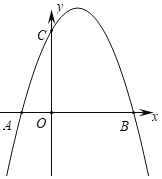
【题目】如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0),OB=OC=3OA.若抛物线L2与抛物线L1关于直线x=2对称.
(1)求抛物线L1与抛物线L2的解析式;
(2)在抛物线L1上是否存在一点P,在抛物线L2上是否存在一点Q,使得以BC为边,且以B、C、P、Q为顶点的四边形为平行四边形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
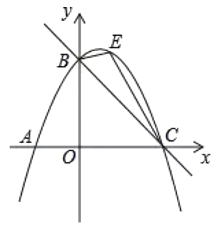
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在课余时间写了三个算式:![]() ,
,![]() ,
,![]() ,通过认真观察,发现任意两个连续奇数的平方差是
,通过认真观察,发现任意两个连续奇数的平方差是![]() 的倍数.
的倍数.
验证
(1)![]() 的结果是
的结果是![]() 的几倍?
的几倍?
(2)设两个连续奇数为![]() ,
,![]() (其中
(其中![]() 为正整数),写出它们的平方差,并说明结果是
为正整数),写出它们的平方差,并说明结果是![]() 的倍数;
的倍数;
延伸
直接写出两个连续偶数的平方差是几的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com