
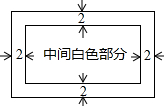
 如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.
如图,小红用一张周长为88cm的长方形白纸做一张贺卡,长方形白纸内部的四周涂上宽为2cm的彩色花边.分析 (1)设原来长方形的长为xcm,则宽为(20-x)cm,则中间部分的长为(x-4)cm,宽为(20-x-4)cm,则花边部分的面积等于原来的面积减去中间部分的面积;
(2)设中间部分的面积为:S求出S与x的关系式,即关于中间部分的面积公式,并求出该二次函数的最大值,即中间部分的最大值,与花边部分的面积相比较,若大于则能做到,小于则做不到.
解答 解:(1)设长方形白纸长为xcm,则宽为(44-x)cm,中间部分的长为(x-2)cm,宽为(44-x-2)cm,
根据题意得:x(44-x)-(x-2)(44-x-2)=84,
答:彩色花边的面积是84cm2.
(2)设长方形白纸长为xcm,则宽为(44-x)cm,
根据题意得:(x-2)(44-x-2)=$\frac{2}{3}$x(44-x),
整理,得
x2-44x+252=0,
解得x1=22+2$\sqrt{58}$,x2=22-2$\sqrt{58}$(舍去),
则44-x=22-2$\sqrt{58}$.
答:长方形白纸的长为(22+2$\sqrt{58}$)cm,宽为(22-2$\sqrt{58}$)cm.
点评 本题主要考查一元二次方程的应用,关键在于理解清楚题意找出等量关系,即:花边部分的面积=总面积-中间部分的面积.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
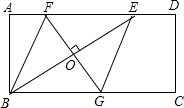 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{3}$AD,连接BE,作BE的垂直平分线分别交AD、BC于点F、G,FG与BE的交点为O,连接BF和EG.
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=$\frac{1}{3}$AD,连接BE,作BE的垂直平分线分别交AD、BC于点F、G,FG与BE的交点为O,连接BF和EG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 200(1+x)2=1000 | B. | 200+200×2x=1000 | ||
| C. | 200(1+x)+200(1+x)2=1000 | D. | 200+200(1+x)+200(1+x)2=1000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com