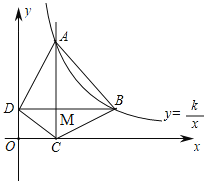
【题目】如图，在平面直角坐标系中，函数
的图象经过点
和点
.过点
作
轴，垂足为点
，过点作
轴，垂足为点
，连结
、
、
、
.点的横坐标为
.
（1）求
的值.
（2）若
的面积为
.
①求点的坐标.
②在平面内存在点
，使得以点、、、为顶点的四边形是平行四边形，直接写出
符合条件的所有点的坐标.
【答案】（1）4；（2）①点
的坐标为
．②
、
、
【解析】
（1）利用待定系数法将A点代入，即可求函数解析式的k值；
（2）用三角形ABD的面积为4,列方程，即可求出a的值,可得点的坐标；
（3）E的位置分三种情况分析，由平行四边形对边平行的关系，用平移规律求对应点的坐标.
（1）
函数
的图象经过点
，
（2）①如图，设AC与BD交与M,
点的横坐标为
，点在
的图象上，
点的坐标为
．
∵
轴，
轴，
∵ ②∵ ∴AC=4 当以ACZ作为平行四边形的边时，BE=AC=4 ∴ ∴ ∴ 当AC作为平行四边形的对角线时，AC中点为 ∴BE中点为（1，2）设E(x，y) ∵点 则 解得： ∴ 综上所述：在平面内存在点 故答案为：
，
． 
的面积为
，
．
． 
．点的坐标为． C(1,0)
、
的坐标为
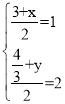
，使得以点
、、
、为顶点的四边形是平行四边形，符合条件的所有点的坐标为：、、、、
名校课堂系列答案科目：初中数学 来源： 题型：
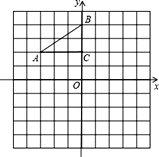
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平面直角坐标系xOy中，点A、B的横坐标分别为a、a+2，二次函数
的图象经过点A、B，且a、m满足2a﹣m=d（d为常数）．
（1）若一次函数y1=kx+b的图象经过A、B两点．
①当a=1、d=﹣1时，求k的值；
②若y1随x的增大而减小，求d的取值范围；
（2）当d=﹣4且a≠﹣2、a≠﹣4时，判断直线AB与x轴的位置关系，并说明理由；
（3）点A、B的位置随着a的变化而变化，设点A、B运动的路线与y轴分别相交于点C、D，线段CD的长度会发生变化吗？如果不变，求出CD的长；如果变化，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一副直角三角尺的直角顶点C叠放在一起．
（1）若∠DCE＝35°，∠ACB＝ ；若∠ACB＝140°，则∠DCE＝ ；
（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；
（3）若保持三角尺BCE不动，三角尺ACD的CD边与CB边重合，然后将三角尺ACD绕点C按逆时针方向任意转动一个角度∠BCD．设∠BCD＝α（0°＜α＜90°）
①∠ACB能否是∠DCE的4倍？若能求出α的值；若不能说明理由．
②三角尺ACD转动中，∠BCD每秒转动3°，当∠DCE＝21°时，转动了多少秒？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①是由五个完全相同的小正方体组成的立体图形，将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )
A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△OAB的顶点坐标分别为O（0，0），A（2，4），B（4，0），分别将点A、B的横坐标、纵坐标都乘以1．5，得相应的点A'、B'的坐标。
（1）画出 OA'B'：
（2）△OA'B'与△AOB______位似图形：（填“是”或“不是”）
（3）若线段AB上有一点
，按上述变换后对应的A'B'上点的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
