
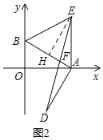
【题目】如图1,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°,以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.
(1)写出点E的纵坐标.
(2)求证:BD=OE;
(3)如图2,连接DE交AB于F.求证:F为DE的中点.

【答案】(1)点E的纵坐标为2;(2)见解析;(3)见解析.
【解析】
(1)直接运用直角三角形30°角的性质和等边三角形的性质可得∠OAE=90°,AE=2;
(2)连接OD,易证△ADO为等边三角形,再证△ABD≌△AEO即可.
(3)作EH⊥AB于H,先证△ABO≌△AEH,得AO=EH,再证△AFD≌△HFE即可.
(1)解:∵点B的坐标为(0,1),
∴OB=1,
∵∠BAO=30°,
Rt△ABO中,AB=2OB=2,
∵△ABE是等边三角形,
∴∠BAE=60°,AE=AB=2,
∴∠OAE=30°+60°=90°,
∴点E的纵坐标为2;
故答案为:2;
(2)证明:连接OD,如图1,

∵△ABE是等边三角形,
∴AB=BE,∠EAB=60°,
∵DA⊥BA,
∴∠DAB=90°,
∵∠BAO=30°,
∴∠DAO=90°﹣30°=60°,
∴∠OAE=∠DAB,
∵MN垂直平分OA,
∴OD=DA,
∴△AOD是等边三角形,
∴DA=OA,
在△ABD和△AEO中,
∵ ,
,
∴△ABD≌△AEO(SAS),
∴BD=OE;
(3)证明:如图2,作EH⊥AB于H,
∴∠EHA=∠DAF=90°,
∵AE=BE,
∴AH=![]() AB,
AB,
∵∠AOB=90°,∠BAO=30°,
∴OB=![]() AB,
AB,
∴AH=BO,
∴Rt△AEH≌Rt△BAO(HL),
∴EH=AO=AD,
∵∠EHF=∠DAF=90°,∠EFH=∠DFA,
∴△HFE≌△AFD(AAS),
∴EF=DF,
∴F为DE的中点.


科目:初中数学 来源: 题型:
【题目】如图所示的函数图象反映的过程是:李大爷每天早上都到公园锻炼,他从家去公园锻炼一会儿,又去了菜市场后马上回家,其中![]() 表示时间,
表示时间,![]() 表示李大爷离他家的距离。
表示李大爷离他家的距离。
(1)李大爷家到公园的距离是多少千米,他在公园银炼了多少小时;
(2)李大爷从菜市场回家的平均速度;
(3)李大爷从家到菜市场的平均速度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知⊙O的半径为 ![]() ,弦AB=2,以AB为底边,在圆内画⊙0的内接等腰△ABC,则底边AB边上的高CD长为( )
,弦AB=2,以AB为底边,在圆内画⊙0的内接等腰△ABC,则底边AB边上的高CD长为( )
A.![]() +1
+1
B.![]() ﹣1
﹣1
C.![]() 或
或 ![]() ﹣1
﹣1
D.![]() +1或
+1或 ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
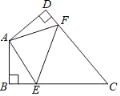
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为( )
A. 90°B. 80°C. 70°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E.
(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(0<x< ![]() ),四边形BPEC的面积为y,求证:y=
),四边形BPEC的面积为y,求证:y= ![]() (
( ![]() ﹣x)2 .
﹣x)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1
(2)点C1的坐标为_________,△ABC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1;
(3)求点A旋转到点A1所经过的路线长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市道路美化工程招标,经测算:甲队 12 天完成的工程量是乙队 9 天完成的工程量的2 倍,甲队干 20 天比乙队干 15 天多完成的工程量占总工程量的![]() .
.
(1)求甲、乙两队一天各完成此项工程的量?
(2)甲队施工一天需付工程款 1.5 万元,乙队施工一天需付工程款 0.8 万元,若要求完成此项工程的工程款不超过 81 万元,则乙队最少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.

根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是________米
(2)小明在书店停留了___________分钟.
(3)本次上学途中,小明一共行驶了________ 米,一共用了______ 分钟.
(4)在整个上学的途中_________(哪个时间段)小明骑车速度最快,最快的速度是___________米/分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com