
分析 根据x3+px+q=(x-a)(x-b)(x-c)且q≠0,展开后得到a,b,c与p,q的关系,当x=a,x=b,x=c时,可以求得a3,b3,c3与p,q的关系,从而可以解答本题.
解答 解:∵x3+px+q=(x-a)(x-b)(x-c)且q≠0,
∴x3+px+q=x3-(a+b+c)x2+(ab+bc+ac)x-abc.
∴a+b+c=0,q=-abc.
∴x=a时,a3+pa+q=0;x=b时,b3+pb+q=0;x=c时,c3+pc+q=0.
∴a3=-pa-q,b3=-pb-q,c3=-pc-q.
∴$\frac{{a}^{3}+{b}^{3}+{c}^{3}}{abc}$=$\frac{-pa-q-pb-q-pc-q}{-q}$=$\frac{-p(a+b+c)-3q}{-q}=\frac{-3q}{-q}=3$.
即$\frac{{a}^{3}+{b}^{3}+{c}^{3}}{abc}$的值是3.
点评 本题考查分式的化简求值,解题的关键是根据题目中的信息找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
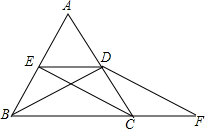 如图,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,问:EC与DF有怎样的位置关系?试说明理由.
如图,已知∠ABC=∠ACB,BD平分∠ABC交AC于点D,CE平分∠ACB交AB于点E,∠DBF=∠F,问:EC与DF有怎样的位置关系?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB,直线y=mx-m恒过定点,且与AB有交点,求m的取值范围$\frac{3}{5}$≤m≤3.
如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连结AB,直线y=mx-m恒过定点,且与AB有交点,求m的取值范围$\frac{3}{5}$≤m≤3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com