Question

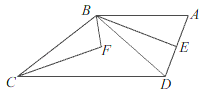
【题目】如图1，平行四边形ABCD，点E在AD上，连接CE，点F为CE中点，连接DF，并且DF＝EF．

（1）求证：平行四边形ABCD是矩形；

（2）如图2，过点B作BH⊥CE，垂足为H，连接AH，若∠AHB＝45°，求证：AE＝CD；

（3）如图3，在（2）的条件下，过点A作AK⊥BH，垂足为N，AK与BC交于点K，若四边形ABHE的面积为128，BK＝2，求线段HF的长度．

Answer 1

【答案】（1）见详解；（2）见详解；（3）

【解析】

（1）根据等腰三角形的性质和三角形内角和即可证明；

（2）过A点作MA⊥AH交HB的延长线于点M，然后证明△ABM≌△AEH即可证明；

（3）连接BE，先根据（2）得到的条件对四边形ABHE的面积进行转换，从而得到AN的的长，设AE=x再根据相似三角形得到BN的表达式，根据勾股定理得到EH的表达式，再把四边形ABHE的面积看作△ABE和△BHE的和，列出方程，解出x的值，再根据已知条件进行计算即可．

（1）∵DF=EF，

∴∠FDE=∠DEF，

又∵DF=FC，

∴∠FDC=∠FCD，

∵∠FDE+∠DEF+∠FDC+∠FCD=180°，即2（∠DEF+∠FCD）=180°，

∴∠EDC=90°，

又∵四边形ABCD是平行四边形，

∴四边形ABCD是矩形；

（2）过A点作MA⊥AH，交HB的延长线于点M，

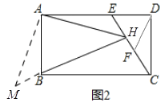
∵MA⊥AH，BH⊥CE，∠AHB=45°，

∴∠AHB=∠AHE=∠AMH=45°，

∴AM=AH，

∵∠MAB+∠BAH=∠EAH+∠BAH=90°

∴∠MAB=∠EAH，

∴△ABM≌△AEH，

∴AB=AE,

由（1）可知四边形ABCD是矩形，

∴AB=CD，

∴AE=CD；

（3）连接BE，

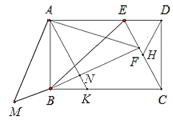
由（2）可知△ABM≌△AEH，

∴S四边形ABHE=S△AMH=128，

∵AH⊥BH，∠AHB=45°，

∴∠KAH=45°，

∴S△ANH是等腰直角三角形，

同理S△AMH是等腰直角三角形，

∴MN=NH=AN（三线合一），

∴S△AMH=2AN·AN·=128，

∴AN=，

∵AK⊥BH，

∴∠ABN+∠BAN=90°，

又∵∠BAN+∠BKA=90°，

∴∠ABN=∠BKA，

又∵∠ABK=∠ANB=90°，

∴△ABN∽△AKB，

设AE=x,

由（2）可知AE=AB=CD=x，

∴，

∴BN=，

则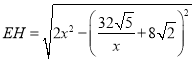

∴，

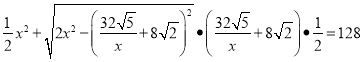解得x=，

由（1）可知四边形ABCD是矩形，

∴AB=CD，∠B=∠D，AD=BC，

∵AN⊥BH，CE⊥BH，

∴AK∥CE，

∴∠CED=∠ECK=∠AKB，

∴△ABK≌△CDE，

∴DE=BK=，

∴，

将x=代入EH的表达式得EH=，

∴HF=EF-EH=．