
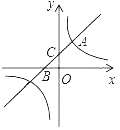
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
【答案】(1)y=![]() ;y=x+1;(2)P点的坐标为(3,0)或(﹣5,0).
;y=x+1;(2)P点的坐标为(3,0)或(﹣5,0).
【解析】
(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;
(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
解:(1)把A(1,2)代入双曲线y=![]() ,可得k=2,
,可得k=2,
∴双曲线的解析式为y=![]() ;
;
把A(1,2)代入直线y=x+b,可得b=1,
∴直线的解析式为y=x+1;
(2)设P点的坐标为(x,0),
在y=x+1中,令y=0,则x=﹣1;令x=0,则y=1,
∴B(﹣1,0),C(0,1),即BO=1=CO,
∵△BCP的面积等于2,
∴![]() BP×CO=2,即
BP×CO=2,即![]() |x﹣(﹣1)|×1=2,
|x﹣(﹣1)|×1=2,
解得x=3或﹣5,
∴P点的坐标为(3,0)或(﹣5,0).


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动:同时点Q沿边AB,BC从点A开始向点C以acm/s的速度移动,当点P移动到点A时,P,Q同时停止移动.设点P出发x秒时,△PAQ的面积为ycm2,y与x的函数图象如图②,线段EF所在的直线对应的函数关系式为y=﹣4x+21,则a的值为( )
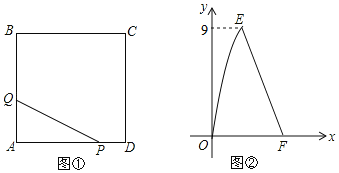
A. 1.5B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
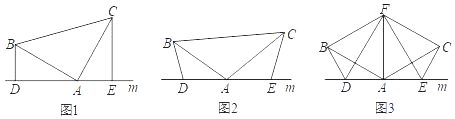
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B |
| 0.25 |
C | 16 | b |
D | 8 |
|
合计 | a | 1 |
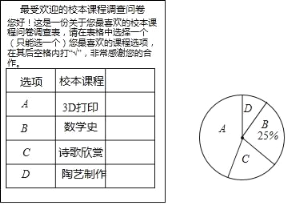
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
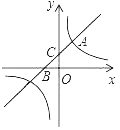
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=-![]() (x+1)(x-a)(a为正数)的图象与x轴交于A、B两点(A在B的左侧),与y轴交于C点.直线l过M(0,m)(0<m<2且m≠1)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数y=-
(x+1)(x-a)(a为正数)的图象与x轴交于A、B两点(A在B的左侧),与y轴交于C点.直线l过M(0,m)(0<m<2且m≠1)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数y=-![]() (x+1)(x-a)的图象关于直线l的对称图象与y轴交于点P.设直线PD与x轴交点为Q,则:
(x+1)(x-a)的图象关于直线l的对称图象与y轴交于点P.设直线PD与x轴交点为Q,则:
(1)求A、C两点的坐标;
(2)求AD的值(用含m的代数式表示);
(3)是否存在实数m,使CDAQ=PQDE?若能,则求出相应的m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
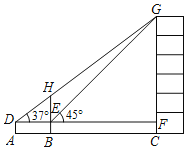
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为37°,此时教学楼顶端G恰好在视线DH上,再向前走8米到达B处,又测得教学楼顶端G的仰角∠GEF为45°,点A、B、C三点在同一水平线上.
(1)求古树BH的高;
(2)计算教学楼CG的高度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
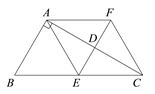
(1)求证:四边形AECF是菱形;
(2)若AB=10,∠ACB=30°,求菱形AECF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com