
【题目】设二次函数y=-![]() (x+1)(x-a)(a为正数)的图象与x轴交于A、B两点(A在B的左侧),与y轴交于C点.直线l过M(0,m)(0<m<2且m≠1)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数y=-
(x+1)(x-a)(a为正数)的图象与x轴交于A、B两点(A在B的左侧),与y轴交于C点.直线l过M(0,m)(0<m<2且m≠1)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数y=-![]() (x+1)(x-a)的图象关于直线l的对称图象与y轴交于点P.设直线PD与x轴交点为Q,则:
(x+1)(x-a)的图象关于直线l的对称图象与y轴交于点P.设直线PD与x轴交点为Q,则:
(1)求A、C两点的坐标;
(2)求AD的值(用含m的代数式表示);
(3)是否存在实数m,使CDAQ=PQDE?若能,则求出相应的m的值;若不能,请说明理由.
【答案】(1)A(-1,0),C(0,2),(2)AD=![]() ;(3)当a>1时,才存在实数m使得△PQA∽△CDE,从而有CDAQ=PQDE,此时m=
;(3)当a>1时,才存在实数m使得△PQA∽△CDE,从而有CDAQ=PQDE,此时m=![]() ;当0<a≤1时,不存在实数m使得CDAQ=PQDE.
;当0<a≤1时,不存在实数m使得CDAQ=PQDE.
【解析】
(1)分别令x=0和y=0代入y=-![]() (x+1)(x-a)中可求得A、C两点的坐标;
(x+1)(x-a)中可求得A、C两点的坐标;
(2)如图1,根据待定系数法求直线AC的解析式,表示点D的坐标,利用勾股定理可得AD的长;
(3)根据∠PQA=∠PDE,和CDAQ=PQDE,可知:△PQA∽△CDE,由对称可知:△CDE≌△PDE,
△PQA∽△PDE,分两种情况进行讨论:
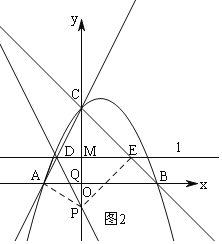
①当0<m<1时,点P在x轴下方,如图2,
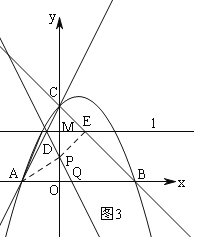
②当1<m<2时,如图3,从相似入手,第一种情况不可能相似所以不成立,第二种情况根据相似列比例式可得m的值.
(1)当x=0时,y=-![]() ×1×(-a)=2,
×1×(-a)=2,
∴点C的坐标为(0,2),
当y=0时,y=-![]() (x+1)(x-a)=0,
(x+1)(x-a)=0,
∴x1=-1,x2=a,
∴点A坐标为(-1,0);
(2)如图1,设直线AC的解析式为:y=kx+b,

把A(-1,0),C(0,2)代入得:![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=2x+2,
∵DM∥x轴,且M(0,m),
∴D(![]() ,m),
,m),
由勾股定理得:AD=![]() =
=![]() ;
;
(3)∵l∥x轴,
∵∠PQA=∠PDE,
当CDAQ=PQDE,即![]() ,
,
则△PQA∽△CDE,
由对称可知:△CDE≌△PDE,
∴△PQA∽△PDE,
分两种情况:
①当0<m<1时,点P在x轴下方,如图2,连接PA和PE,
此时∠PQA显然为钝角,
而∠PDE显然为锐角,故此时不能有△PQA∽△CDE.
②当1<m<2时,如图3,连接PA和PE,
∵M(0,m),
∴OM=m,
∴CM=2-m,
∵CM=PM=2-m,
∴OP=OM-PM=m-(2-m)=2m-2,
∵△APQ∽△EPD,
∴![]() ,
,
∵D(![]() ,m),P(0,2m-2),
,m),P(0,2m-2),
易得DP的解析式为:y=-2x+2m-2,
当y=0时,-2x+2m-2=0,
x=m-1,
∴Q(m-1,0),
∴AQ=1+m-1=m,
∵B(a,0),C(0,2),
易得直线BC的解析式为:y=-![]() x+2,
x+2,
当y=m时,-![]() x+2=m,
x+2=m,
x=![]() ,
,
∴E(![]() ,m),
,m),
∴DE=![]()
![]() =
=![]() ,
,
∴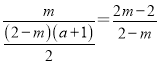 ,
,
∴m=![]() ,而此时1<m<2,
,而此时1<m<2,
则应有1<![]() <2,由此知a>1.
<2,由此知a>1.
综上所述,当a>1时,才存在实数m使得△PQA∽△CDE,从而有CDAQ=PQDE,此时m=![]() ;当0<a≤1时,不存在实数m使得CDAQ=PQDE.
;当0<a≤1时,不存在实数m使得CDAQ=PQDE.


科目:初中数学 来源: 题型:
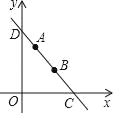
【题目】如图,在平面直角坐标系中,过点A![]() 的直线l分别与x轴、y轴交于点C,D.
的直线l分别与x轴、y轴交于点C,D.
(1)求直线l的函数表达式.
(2)P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.
(3)将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
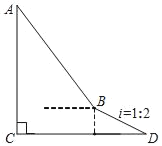
【题目】如图,为了测量建筑物AC的高度,从距离建筑物底部C处50米的点D(点D与建筑物底部C在同一水平面上)出发,沿坡度i=1:2的斜坡DB前进10![]() 米到达点B,在点B处测得建筑物顶部A的仰角为53°,求建筑物AC的高度.(结果精确到0.1米.参考数据:sin53°≈0.798,cos53°≈0.602,tan53°≈1.327.)
米到达点B,在点B处测得建筑物顶部A的仰角为53°,求建筑物AC的高度.(结果精确到0.1米.参考数据:sin53°≈0.798,cos53°≈0.602,tan53°≈1.327.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
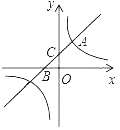
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生的安全意识,在全校范围内随机抽取部分学生进行问卷调查.根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.
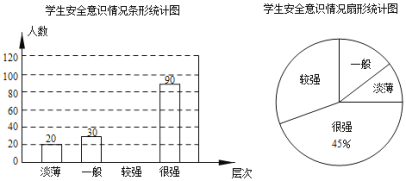
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,将条形统计图补充完整;
(2)扇形统计图中,“较强”层次所占圆心角的大小为 °;
(3)若该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,请你估计全校需要强化安全教育的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
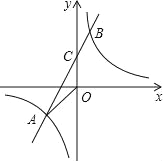
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的解析式;
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲市到乙市乘坐高铁列车的路程为180千米,乘坐普通列车的路程为240千米,高铁列车的平均速度是普通列车的平均速度的3倍,高铁列车的乘车时间比普通列车的乘车时间缩短了2小时.
(1)求高铁列车的平均速度是每小时多少千米;
(2)某日王老师要去距离甲市大约405m的某地参加14:00召开的会议,如果他买到当日10:40从甲市至该地的高铁票,而且从该地高铁站到会议地点最多需要1.5h,试问在高铁列车准点到达的情况下他能在开会之前到达吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
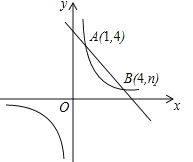
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com