
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(-2,0)和点B,与y轴交于C,对称轴为直线x=![]() .
.
(1)求a、b满足的关系式;
(2)若点D为抛物线的顶点,连接CD,DB,BC,S△BCD= ![]() .
.
①求抛物线的解析式;
②点M是第一象限内对称轴右侧抛物线上一点,过点M作MN⊥x轴,垂足为点N,线段MN上有一点H,若∠HBA+∠MAB=90°,求证:HN的长为定值.
【答案】(1)a+b=0;(2)① y=a(x+2)(x-3);②见解析
【解析】
(1)根据抛物线的对称轴公式即可求出a、b的关系;
(2)①先求出抛物线与x轴的两个交点,用交点式设出函数解析式,再根据S△BCD= ![]() 求出a即可;
求出a即可;
②先证△BNH ∽△MNA,根据相似三角形的性质列出比例式,设M(t,-t2+t+6),则N(t,0),代入计算即可.
(1)∵抛物线的对称轴为直线x=![]() ,
,
∴-![]() =
=![]() ,
,
即b=-a,
∴a、b满足的关系式为a+b=0
(2)①∵抛物线y=ax2+bx+c(a<0)的对称轴为直线x=![]() ,
,
且抛物线与x轴的一个交点A的坐标为(-2,0),
∴抛物线与x轴的另一个交点B的坐标为(3,0).
设抛物线的解析式为y=a(x+2)(x-3),
即y=ax2-ax-6a,
当x=0时,y=-6a,
∴C(0,-6a),
设直线BC的解析式为y=kx+m,
将B(3,0),C(0,-6a)代入直线BC的解析式得,
![]() ,解得
,解得![]() ,
,
∴直线BC的解析式为y=2ax-6a
如图,设直线BC交抛物线的对称轴于点E,
∴E(![]() ,-5a),D(
,-5a),D(![]() ,-
,-![]() ),
),
∴DE=-![]() a-(-5a)=-
a-(-5a)=-![]() a,
a,
∵S△BCD=S△BDE+S△CED
=![]() DE·(xB-xC)
DE·(xB-xC)
=![]() ×(-
×(-![]() )×3
)×3
=-![]() ,
,
∵S△BCD=![]() ,
,
∴a=-1,
∴抛物线的解析式为y=-x2+x+6
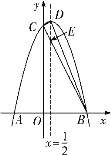
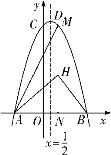
②如图,
∵A(-2,0),B (3,0),MN⊥x轴,
∴∠HNB =∠ANM =90°,
∴∠BHN +∠HBN =90°,
又∵∠HBA+∠MAB=90°,
∴∠BHN =∠MAB,
∴△BNH ∽△MNA,
∴![]() =
=![]()
设M(t,-t2+t+6),则N(t,0),
∴![]() =
=![]() ,
,
∴HN=![]() =
=![]() =1,
=1,
∴HN的长为定值


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
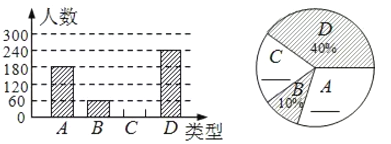
【题目】端午节吃粽子是我国的传统习俗,某食品厂为了解某市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成下面的两幅统计图甲、乙(尚不完整),请根据图中信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)若有外形完全相同的A,B,C,D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取到最大值,则最大值为 ;(用含a、b的式子表示)。
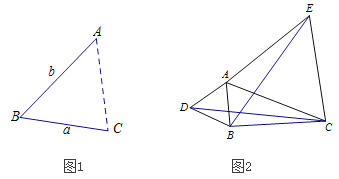
(2)如图2,若点A为线段BC外一动点,且BC=4,AB=2,分别以AB,AC为边,作等边![]() 和等边
和等边![]() ,连接CD,BE.
,连接CD,BE.
①图中与线段BE相等的线段是线段 ,并说明理由;
②直接写出线段BE长的最大值为 。
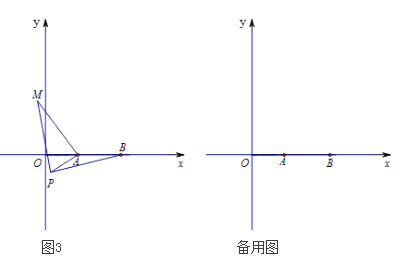
(3)如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值为 ,及此时点P的坐标为 。(提示:等腰直角三角形的三边长a、b、c满足a:b:c=1:1:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年九龙口诗词大会在九龙口镇召开,我校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.
(1)若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;
(2)若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A是双曲线y=-![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,点C在第一象限,且∠ACB=120°,点C的位置随着点A的运动在不断变化,但始终在双曲k线y=
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,点C在第一象限,且∠ACB=120°,点C的位置随着点A的运动在不断变化,但始终在双曲k线y=![]() 上,则k的值为_______.
上,则k的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
(1)(收集数据)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是________.
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
(2)(整理数据)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
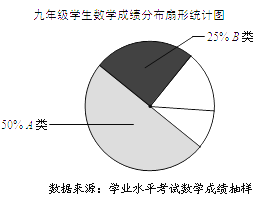
①C类和D类部分的圆心角度数分别为________°、________°;
②估计九年级A、B类学生一共有________名.
(3)(分析数据)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
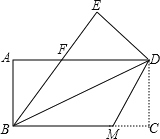
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:如图1,圆的概念:在平面内,线段![]() 绕它固定的一个端点
绕它固定的一个端点![]() 旋转一周,另一个端点
旋转一周,另一个端点![]() 所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在
所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在![]() ,半径为
,半径为![]() 的圆的方程可以写为:
的圆的方程可以写为:![]() , 如:圆心在
, 如:圆心在![]() ,半径为5的圆方程为:
,半径为5的圆方程为:![]()
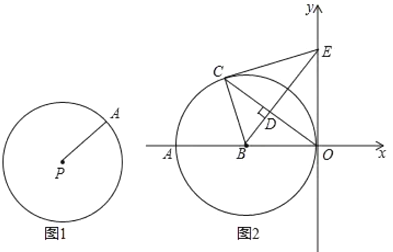
(1)填空:以![]() 为圆心,
为圆心,![]() 为半径的圆的方程为______;
为半径的圆的方程为______;
(2)根据以上材料解决下列问题:如图2, 以![]() 为圆心的圆与
为圆心的圆与![]() 轴相切于原点,
轴相切于原点,![]() 是
是![]() 上一点,连接
上一点,连接![]() ,作
,作![]() 垂足为
垂足为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,已知
,已知![]() .
.
①连接![]() ,证明
,证明![]() 是
是![]() 的切线;
的切线;
②在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 点坐标,并写出以
点坐标,并写出以![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com