练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在△ABC中，D为AB边上一点，∠B=∠ACD，若AD=4，BD=3，求AC的长．
    考点：相似三角形的判定与性质
    专题：
    分析：由条件可证得△ABC∽△ACD，可得到
    AC
    AD
    =
    AB
    AC
    ，从而可求得AC的长．
    解答：证明：∵∠B=∠ACD，
    又∴∠A=∠A，
    ∴△ABC∽△ACD，
    ∵
    AC
    AD
    =
    AB
    AC
    ，
    ∴AC2=AD•AB．
    ∵AD=4，BD=3，
    ∴AB=7，
    ∴AC=2
    		7
    ．
    点评：本题主要考查相似三角形的判定和性质，掌握利用两组角对应相等可判定两个三角形相似是解题的关键，把线段的乘积化为比例来证明是解这类问题的一般思路．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    甲，乙两同学都是邻居，在某个季度里他们相约到一家商店去买若干次白糖，两人买糖的方式不同，甲每次总是买一千克白糖，乙每次总是买一元钱白糖，而白糖的价格总是变动的，试问这两同学买白糖的方式哪一种比较合算？
    先弄清什么叫合算．单看这个季度是谁买的白糖多或谁花的钱少都不对，应计算各人平均每千克白糖花多少钱（单价），单价低的就合算，按下列过程填空回答：
    设两人相约买了n次白糖（n＞1），各次白糖的价格分别为x1，x2，…xn（元/千克）．
    甲共买白糖
     
    千克，总计花去
     
    元，平均每千克白糖的单价是a=
     
    ．
    乙共买白糖
     
    千克，总计花去
     
    元，平均每千克白糖的单价是b=
     
    ．
    试设计一组具体的数据，比较a，b的大小，再据此猜想在一般情况下，谁比较合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=1，DC=2，点P是AB上的动点，则PC+PD的最小值为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

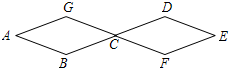    如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动，行走2015厘米后停下，则这只蚂蚁停在（　　）
    A、B点B、C点C、G点D、E点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）[x（x2y2-xy）-y（x2-x3y）]÷3x2y
    （2）（x+3）（x+4）-（x-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：（x-1）2=2（x2-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，PA⊥OA于点A，PB⊥OB于点B，你认为再添加下列哪个条件也不能推出OP垂直平分AB（　　）
    A、OP⊥AB
    B、OP平分∠AOB
    C、PA=PB
    D、∠OPA=∠OPB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    老师布置了一道考题：如图所示，点M、N分别在正△ABC的边BC、CA上，且BM=CN，AM交BN于点Q．
    （1）求证：∠BQM=60°；
    （2）做完（1）后，同学们在老师的启发下进行了反思和探究，得出如下许多结论：
    ①若将题中的“BM=CN”与∠BQM=60°位置交换，则命题正确；
    ②若将题中的点M、N分别移动到BC、CA的延长线上，直线AM、BN交点为Q，则∠BQM=60°；
    ③若将题中的条件“点M、N分别在正△ABC的边BC、CA上”改为“点M、N分别在正方形ABCD的边BC、CD上”，且BM=CN，AM交BN于点Q，则∠BQM=90°；
    ④把③中的“BM=CN”与∠BQM=90°的位置互换，则命题正确；
    …
    请你判断上述四个结论正确的有
     
    （填序号即可）
    选择其中的一个结论给出你的证明（自己画出图形，然后结合图形证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    把两个完全相同的矩形按如图所示的方式叠合起来；若矩形的长与宽分别为8cm与6cm，则重叠部分的面积为
     
    cm2．

    查看答案和解析>>

    同步练习册答案