
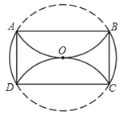
【题目】如图,在⊙O中,分别将弧AB、弧CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,若⊙O的半径为4,则四边形ABCD的面积是__________________.
【答案】![]()
【解析】
作OH⊥AB,延长OH交![]() 于E,反向延长OH交CD于G,交
于E,反向延长OH交CD于G,交![]() 于F,连接OA、OB、OC、OD,根据折叠的对称性及三角形全等,证明AB=CD,又因AB∥CD,所以四边形ABCD是平行四边形,由平行四边形面积公式即可得解.
于F,连接OA、OB、OC、OD,根据折叠的对称性及三角形全等,证明AB=CD,又因AB∥CD,所以四边形ABCD是平行四边形,由平行四边形面积公式即可得解.
如图,作OH⊥AB,垂足为H,延长OH交![]() 于E,反向延长OH交CD于G,交
于E,反向延长OH交CD于G,交![]() 于F,连接OA、OB、OC、OD,则OA=OB=OC=OD=OE=OF=4,
于F,连接OA、OB、OC、OD,则OA=OB=OC=OD=OE=OF=4,
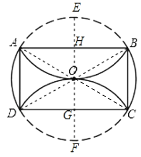
∵弧AB、弧CD沿两条互相平行的弦AB、CD折叠,折叠后的弧均过圆心,
∴OH=HE=![]() ,OG=GF=
,OG=GF=![]() ,即OH=OG,
,即OH=OG,
又∵OB=OD,
∴Rt△OHB≌Rt△OGD,
∴HB=GD,
同理,可得AH=CG= HB=GD
∴AB=CD
又∵AB∥CD
∴四边形ABCD是平行四边形,
在Rt△OHA中,由勾股定理得:
AH=![]()
∴AB=![]()
∴四边形ABCD的面积=AB×GH=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
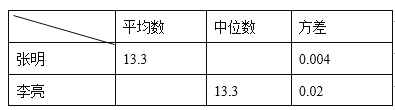
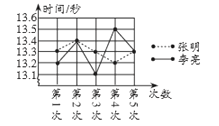
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上运动,且
轴的正半轴上运动,且![]() ,下列结论:
,下列结论:
①![]()
②当![]() 时四边形
时四边形![]() 是正方形
是正方形
③四边形![]() 的面积和周长都是定值
的面积和周长都是定值
④连接![]() ,
,![]() ,则
,则![]() ,其中正确的有( )
,其中正确的有( )
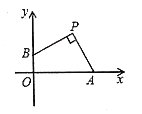
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情爆发,某企业准备转型生产口罩.该企业在市场上物色到两种生产![]() 口罩的设备,若采购2台
口罩的设备,若采购2台![]() 型设备,5台
型设备,5台![]() 型设备则共需要430万元;若采购5台
型设备则共需要430万元;若采购5台![]() 型设备,2台
型设备,2台![]() 型设备则共需要550万元.已知
型设备则共需要550万元.已知![]() 型设备每台每天可以生产19万片
型设备每台每天可以生产19万片![]() 口罩;
口罩;![]() 型设备每台每天可以生产8万片
型设备每台每天可以生产8万片![]() 口罩.
口罩.
(1)求![]() 、
、![]() 两型设备的采购单价分别是多少万元/台?
两型设备的采购单价分别是多少万元/台?
(2)该企业准备采购![]() 、
、![]() 两型设备共10台,但能用来采购设备的资金不超过700万元,那么如何安排采购方案,用这些设备每天生产的
两型设备共10台,但能用来采购设备的资金不超过700万元,那么如何安排采购方案,用这些设备每天生产的![]() 口罩最多?每天最多可生产多少万片
口罩最多?每天最多可生产多少万片![]() 口罩?
口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:![]() . 设这种产品每天的销售利润为w元.
. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
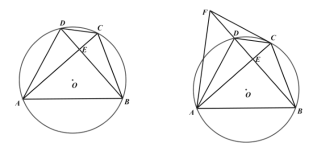
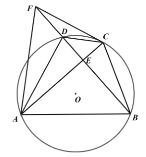
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形.![]() .反比例函数
.反比例函数![]() 在第一象限内的图象经过点A,交BC的中点F.且
在第一象限内的图象经过点A,交BC的中点F.且 ![]() .
.
(1)求k值和点C的坐标;
(2)过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
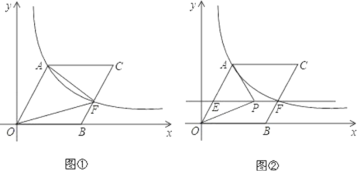
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com