
【题目】如图,一次函数![]() 的图像与坐标轴交于A、B两点,点C的坐标为
的图像与坐标轴交于A、B两点,点C的坐标为![]() ,二次函数
,二次函数![]() 的图像经过A、B、C三点.
的图像经过A、B、C三点.
(1)求二次函数的解析式
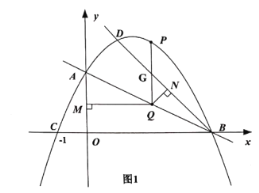
(2)如图1,已知点![]() 在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作
在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作![]() 轴于点M,作
轴于点M,作![]() 于点N,过Q作
于点N,过Q作![]() 轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足![]() ,求点E的坐标.
,求点E的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)求出A、B的坐标,设二次函数解析式为![]() ,把A(0,2)代入即可得出结论;
,把A(0,2)代入即可得出结论;
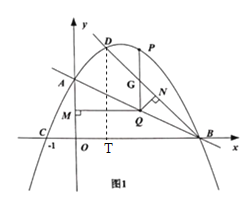
(2)先求出D的坐标和直线BD的解析式,过D作DT⊥x轴于T,可求得∠DBO=45°.设Q(m,![]() m+2),则G(m,-m+4),MQ=m.设∠ABO=α,则∠NBQ=45°-α,∠MQB=180°-α.证明ΔGQN为等腰直角三角形,表示出NQ,MQNQ,利用二次函数的性质解答即可;
m+2),则G(m,-m+4),MQ=m.设∠ABO=α,则∠NBQ=45°-α,∠MQB=180°-α.证明ΔGQN为等腰直角三角形,表示出NQ,MQNQ,利用二次函数的性质解答即可;
(3)如图,过A作AH⊥PE于点H,解Rt△APH,得到AH=1,PH=2.设H(m,n),利用两点间距离公式可求出H的坐标,进而求出点E的坐标.
(1)在![]() 中,令x=0,得y=2,∴A(0,2);
中,令x=0,得y=2,∴A(0,2);
令y=0,得![]() ,解得:x=4,∴B(4,0).
,解得:x=4,∴B(4,0).
设二次函数解析式为![]() ,
,
将A(0,2)代入得:
![]()
解得:![]() ,
,
∴![]() .
.
(2)∵点D(1,n)在抛物线上,∴n=![]() =3,
=3,
∴D(1,3).
设直线BD的解析式为y=kx+b,则![]() ,
,
解得:![]() ,
,
∴直线BD的解析式为:y=-x+4.
过D作DT⊥x轴于T,则OT=1,DT=3.
∵OB=4,∴BT=OB-OT=4-1=3,
∴DT=BT,
∴∠DBO=45°.
 设Q(m,
设Q(m,![]() m+2),则G(m,-m+4),MQ=m.
m+2),则G(m,-m+4),MQ=m.
设∠ABO=α,则∠NBQ=45°-α
∠MQB=180°-α.
又∵∠PQM=90°,∠NQB=90°-(45°-α)=45°+α,
∴∠GQN=360°-90°-(180°-α)-(45°+α)=45°,
∴ΔGQN为等腰直角三角形,
∴NQ=![]()
![]() ,
,
∴MQNQ=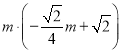
![]() .
.
当m=2时,QMQN最大,此时P(2,3).
(3)如图,过A作AH⊥PE于点H,其中,∠APE=∠ABO.
又A(0,2),P(2,3),
![]() ,
,
∴![]() ,
,
∴PH=2AH.
∵AP=![]() ,
,![]() ,
,
∴![]() ,
,
∴AH=1,PH=2.
设H(m,n),
则![]() ,
,
![]() ,
,
解得:![]() ;
;![]() ,
,
∴![]() ,
,![]() .
.
①易求直线PH的解析式为![]() :
:![]()
令![]()
解得:![]() (舍)
(舍)
∴![]() ;
;
②易求直线PH1的解析式为![]() :
:![]() .
.
令![]() ,
,
解得:![]() ,
,
∴![]() .
.
综上所述:符合题意的E点坐标为![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
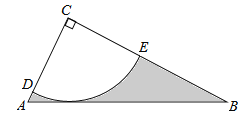
【题目】如图,在Rt△ABC中,∠C=90°,AC![]() ,tanB
,tanB![]() ,半径为2的⊙C分别交AC,BC于点D、E,得到DE弧.
,半径为2的⊙C分别交AC,BC于点D、E,得到DE弧.
(1)求证:AB为⊙C的切线.
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
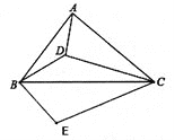
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学为了解学生对食堂工作的满意程度,8年级2班数学兴趣小组在全校甲、乙两个班内进行了调查统计,将调查结果分为不满意、一般、满意、非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.


请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数;
(2)求此次调查中结果为非常满意的人数;
(3)兴趣小组准备从调查结果为一般的4位同学中随机选择2位进行回访,已知4位同学中有2位来自甲班,另2位来自乙班,请用列表或用画树状图的方法求出选择的同学均来自甲班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点C在
,点C在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点C作
,过点C作![]() 于点F,交
于点F,交![]() 于点G,过C作
于点G,过C作![]() 交
交![]() 的延长线于点E.
的延长线于点E.
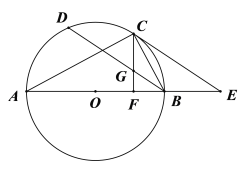
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
我们通过下列步骤估计方程2x2+x﹣2=0的根的所在的范围.
第一步:画出函数y=2x2+x﹣2的图象,发现图象是一条连续不断的曲线,且与x轴的一个
交点的横坐标在0,1之间.
第二步:因为当x=0时,y=﹣2<0;当x=1时,y=1>0.
所以可确定方程2x2+x﹣2=0的一个根x1所在的范围是0<x1<1.
第三步:通过取0和1的平均数缩小x1所在的范围;
取x=![]() ,因为当x=
,因为当x=![]() 时,y<0,
时,y<0,
又因为当x=1时,y>0,
所以![]() <x1<1.
<x1<1.
(1)请仿照第二步,通过运算,验证2x2+x﹣2=0的另一个根x2所在范围是﹣2<x2<﹣1;
(2)在﹣2<x2<﹣1的基础上,重复应用第三步中取平均数的方法,将x2所在范围缩小至m<x2<n,使得n﹣m≤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )

A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏东70o方向上,轮船从A处以每小时30海里的速度沿南偏东50o方向匀速航行,1小时后到达码头B处,此时观测灯塔C位于北偏东25o方向上,求灯塔C与码头B之间的距离(结果保留根号).
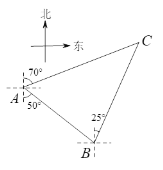
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com