
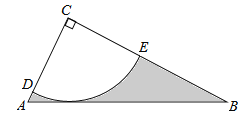
【题目】如图,在Rt△ABC中,∠C=90°,AC![]() ,tanB
,tanB![]() ,半径为2的⊙C分别交AC,BC于点D、E,得到DE弧.
,半径为2的⊙C分别交AC,BC于点D、E,得到DE弧.
(1)求证:AB为⊙C的切线.
(2)求图中阴影部分的面积.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,下列结论中错误的有( )
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
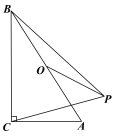
【题目】在Rt△ACB中,C为直角顶点,∠ABC=25°,O为斜边AB的中点,将OA绕着点O逆时针旋转α(0°<α<180°)到OP.当△BCP为等腰三角形时,α的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
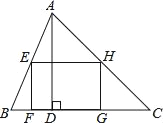
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=![]() EH.
EH.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
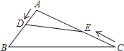
【题目】如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
A. 3或2.8 B. 3或4.8 C. 1或4 D. 1或6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)证明:无论m为何值方程都有两个实数根;
(2)是否存在正数m,使方程的两个实数根的平方和等于26?若存在,求出满足条件的正数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
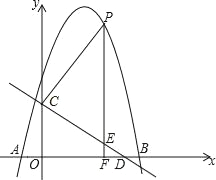
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以PQCD为顶点的四边形是平行四边形是否存在?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com