
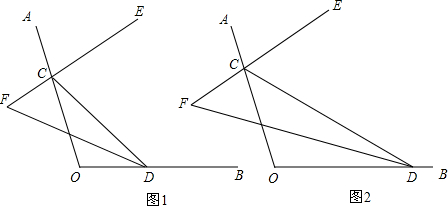
分析 (1)根据三角形的内角和是180°,可求∠CDO=40°,所以∠CDF=20°,又由平角定义,可求∠ACD=150°,所以∠ECD=75°,又根据三角形的外角等于与它不相邻的两内角之和,可求∠ECD=∠F+∠CDF,∠F=55°.
(2)同理可证,∠F=45度.
解答 解:(1)∵∠AOB=110°∠OCD=30°,
∴∠CDO=40°.
∵CE是∠ACD的平分线DF是∠CDO的平分线,
∴∠ECD=75°,∠CDF=20°.
∵∠ECD=∠F+∠CDF,
∴∠F=55°.
(2)不变化,∠F=55°.
∵∠AOB=110°,
∴∠CDO=110°-∠OCD,∠ACD=180°-∠OCD,
∵CE是∠ACD的平分线,DF是∠CDO的平分线,
∴∠ECD=110°-$\frac{1}{2}$∠OCD,∠CDF=55°-$\frac{1}{2}$∠OCD.
∵∠ECD=∠F+∠CDF,
∴∠F=55°.
点评 本题考查了三角形的外角等于与它不相邻的两内角之和,以及三角形的内角和是180°的定理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
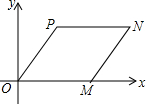 如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )
如图所示,在平面直角坐标系中,菱形OMNP的顶点P的坐标为(3,4),则顶点N的坐标是( )| A. | (7,4) | B. | (8,4) | C. | (9,4) | D. | (10,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
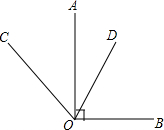 已知,如图,OA⊥BO于点O,OC是∠AOB外部一条射线,且∠AOC=40°,又OD平分∠COB,求∠AOD的度数.
已知,如图,OA⊥BO于点O,OC是∠AOB外部一条射线,且∠AOC=40°,又OD平分∠COB,求∠AOD的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com